Entrar Página Discusión Historial Go to the site toolbox

Energía electrostática de un sistema de cargas puntuales

De Laplace

Contenido

1 Enunciado

Halle la energía electrostática almacenada en los siguientes sistemas de cargas puntuales:

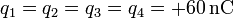  1. q_1=q_2=q_3=q_4=+60\,\mathrm{nC}.
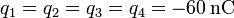  2. q_1=q_2=q_3=q_4=-60\,\mathrm{nC}.
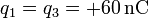  3. q_1=q_3=+60\,\mathrm{nC}, q_2=q_4=-60\,\mathrm{nC}.
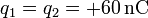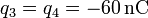  4. q_1=q_2=+60\,\mathrm{nC}, q_3=q_4=-60\,\mathrm{nC}.
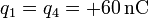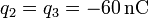  5. q_1=q_4=+60\,\mathrm{nC}, q_2=q_3=-60\,\mathrm{nC}.

situadas en cada caso en los vértices de un rectángulo

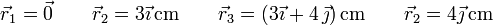
\vec{r}_1 = \vec{0}\qquad \vec{r}_2 = 3\vec{\imath}\,\mathrm{cm}\qquad \vec{r}_3 = (3\vec{\imath}+4\,\vec{\jmath})\,\mathrm{cm}\qquad \vec{r}_2 = 4\vec{\jmath}\,\mathrm{cm}

2 Introducción

La energía de un sistema de cargas puntuales se calcula mediante la fórmula

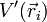U = \frac{1}{2}\sum_i q_i V'(\vec{r}_i)

Siendo V'(\vec{r}_i) el potencial creado por el resto de las cargas en la posición de la carga i. A su vez, este potencial viene dado por la suma

V'(\vec{r}_i)=\frac{1}{4\pi\varepsilon_0}\sum_{k\neq i}\frac{q_k}{d_{ik}}

siendo dik la distancia entre qi y qk.

En este problema las posiciones son las mismas en todos los casos. Las distancias respectivas valen

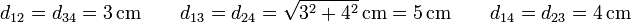
d_{12}=d_{34}=3\,\mathrm{cm}\qquad d_{13}=d_{24}=\sqrt{3^2+4^2}\,\mathrm{cm}=5\,\mathrm{cm}\qquad d_{14}=d_{23}=4\,\mathrm{cm}

Llevando la expresión del potencial a la de la energía queda

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): U = \frac{1}{8\pi\varepsilon_0}\left(q_1\left(\frac{q_2}{d_{12}}+\frac{q_3}{d_{13}}+\frac{q_4}{d_{14}}}\right)+q_1\left(\frac{q_2}{d_{12}}+\frac{q_3}{d_{13}}+\frac{q_4}{d_{14}}}\right)\right. +\\ \left.q_1\left(\frac{q_2}{d_{12}}+\frac{q_3}{d_{13}}+\frac{q_4}{d_{14}}}\right)+q_1\left(\frac{q_2}{d_{12}}+\frac{q_3}{d_{13}}+\frac{q_4}{d_{14}}}\right)\right)

3 Primer caso

4 Segundo caso

5 Tercer caso

6 Cuarto caso

7 Quinto caso

8 Resumen

Obtenido de "http://tesla.us.es/wiki/index.php/Energ%C3%ADa_electrost%C3%A1tica_de_un_sistema_de_cargas_puntuales"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace