Trabajo realizado para reunir cuatro cargas puntuales (F2GIA)

De Laplace

1 Enunciado

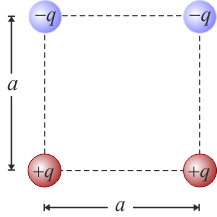
Un sistema electrostático está formado por dos cargas puntuales de valor + q y otras dos − q, situadas en los vértices de un cuadrado de lado a. Las cargas están dispuestas de manera que en los extremos de cada diagonal del cuadrado hay cargas de distinto signo, tal como se muestra en la figura. Calcular el trabajo externo que ha sido necesario realizar para configurar dicho sistema trayendo las cargas desde el infinito.

2 Solución

Para constituir el sistema electrostático bajo estudio procedereremos a traer las cargas, una a una, siguiendo una secuencia de cuatro procesos. En cada uno de ellos, la carga que se traslada estará sometida a la fuerza externa y a la fuerza que ejerce sobre ella el campo eléctrico creado por las cargas traídas previamente. Además, procuraremos que dichos procesos sean (casi)estacionarios. Es decir, procesos (casi)ideales en los que la disipación de energía por fricción o rozamiento es (casi)nula, y la energía cinética del sistema no sufre variaciones apreciables. Por tanto, en cada instante de tiempo se tendrá que los trabajos infinitesimales realizados por la fuerza externa aplicada y por el campo eléctrico que actúa sobre la carga q_i transportada, son opuestos. Y como la fuerza realizada por un campo eléctrico creado por cargas en reposo es conservativa, se tendrá que el trabajo elemental de la fuerza externa va a coincidir con la variación que experimenta la energía potencial de la partícula cargada q_ial desplazarse una cantidad infinitesimal en el seno del campo eléctrico creado por las cargas previamente reunidas:

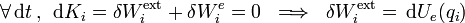
evitaremos fenómenos de disipación de energía procuraremos que no haya disipación de energía