Condensador plano de capacidad ajustable GIA

De Laplace

1 Enunciado

Las armaduras de un condensador plano tienen una superficie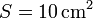 y están separadas una distancia 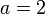mm. El condensador se carga con una batería de 9 V y después se desconecta de la batería. A continuación se coloca una placa de material dieléctrico de espesor 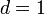mm y de constante dieléctrica κ = 2 pegada a una de sus armaduras. Calcular:

1. Carga eléctrica en cada armadura del condensador.
2. Capacidad del condensador con el dieléctrico.
3. Distancia adicional que deben separarse las armaduras del condensador después de introducir el dieléctrico para que su capacidad sea la misma que tenía antes de introducir el dieléctrico.
4. Energía electrostática almacenada en el condensador relleno de aire, con la placa dieléctrica y después de separar las armaduras.

2 Solución

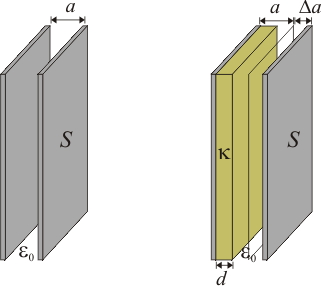
En el sistema de conductores planos descrito, la distancia a de separación entre las placas es considerablemente menor que las dimensiones de los conductores. Considerando que éstos fueran aproximadamente cuadrados, y con los valores indicados en el enunciado, se tendría que la relación entre las longitudes de los lados de las armaduras metálicas y la distancia que las separa es del orden de...

suficiente para considerar en primera aproximación que, una vez cargados los planos conductures y alejados de otras distrubciondes de carga, aquéllos se van a encontrar en influencia total. Es decir, todas las líneas del campo eléctrico que salen de una placa terminan en la otra, de manera que ambas van a almacenar cantidades opuestas de carga, Q y − Q. Además, podemos considerar que la carga eléctrica se distribuirá casi uniformemente en cada una de las superficies interiores (enfrentadas) de las placas conductoras, pudiendo despreciarse los efectos de acumulación de carga eléctrica en los bordes. Es decir, el sistema bajo estudio se aproxima bastante al modelo ideal de condensador plano paralelo, cuya capacidad eléctrica (es decir, la relación entre la carga en uno de los conductores y al diferencia de potencial entre ambos), es

 

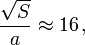
cuando las placas o armaduras conducturas de sección S están separadas por una distancia a vacía (ausente de cualquier medio material)

2.1 Carga eléctrica en las armaduras