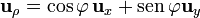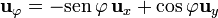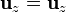Entrar Página Discusión Historial Go to the site toolbox

Relaciones entre las bases vectoriales

De Laplace

Contenido

1 De cartesianas a cilíndricas

  • \mathbf{u}_\rho = \cos\varphi\,\mathbf{u}_{x} + \mathrm{sen}\,\varphi \mathbf{u}_{y}
  • \mathbf{u}_\varphi = -\mathrm{sen}\,\varphi\,\mathbf{u}_{x} + \cos\varphi \mathbf{u}_{y}
  • \mathbf{u}_z=\mathbf{u}_z\,

2 De cartesianas a esféricas

3 De cilíndricas a cartesianas

4 De cilíndricas a esféricas

5 De esféricas a cartesianas

6 De esféricas a cilíndricas

A su vez, todas estas expresiones pueden expresarse en los diferentes sistemas de coordenadas, sustituyendo las relaciones entre las distintos sistemas de coordenadas

7 Artículo siguiente

El vector de posición y otros ejemplos

8 Artículo anterior

Coordenadas esféricas. Base vectorial

Obtenido de "http://tesla.us.es/wiki/index.php/Relaciones_entre_las_bases_vectoriales"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace