Entrar Página Discusión Historial Go to the site toolbox

Variación de entropía a volumen y presión constante

De Laplace

Contenido

1 Enunciado

Un cilindro de 20 cm de diámetro contiene aire inicialmente a 300 K, siendo la presión externa de 100 kPa. En el cilindro se encuentra un émbolo situado inicialmente a 15 cm de distancia del fondo. Se sumerge el cilindro en un baño térmico a 450 K. Calcule la variación de entropía del gas, del entorno y del universo si:

  1. El émbolo está atornillado en su posición.
  2. El émbolo puede deslizarse libremente.

2 A volumen constante

En el primer caso tenemos que el calor se le cede al gas, manteniendo éste constante su volumen.

El volumen inicial (y final del gas) vale

V = \pi r^2 h = \pi\times 0.10^2\times 0.15\,\mathrm{m}^3 = 4.71\times 10^{-3}\,\mathrm{m}^3

y el número de moles de gas es

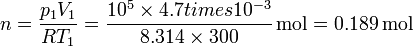
n = \frac{p_1V_1}{RT_1} = \frac{10^5\times 4.7ºtimes 10^{-3}}{8.314\times 300}\,\mathrm{mol}=0.189\,\mathrm{mol}
Entropía del gas
Hallamos la variación de la entropía a partir de la fórmula para un gas ideal en función de T y V (para aprovechar que V no cambia)
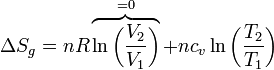
\Delta S_g = n R\overbrace{\ln\left(\frac{V_2}{V_1}\right)}^{=0}+n c_v\ln\left(\frac{T_2}{T_1}\right)
Por comportarse el aire como un gas diatómico
c_v \simeq \frac{5}{2}R = 20.8\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}
lo que da la variación de entropía
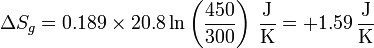
\Delta S_g = 0.189\times 20.8\ln\left(\frac{450}{300}\right)\,\frac{\mathrm{J}}{\mathrm{K}} = +1.59 \,\frac{\mathrm{J}}{\mathrm{K}}
Entropía del entorno
Variación total

3 A presión constante

Obtenido de "http://tesla.us.es/wiki/index.php/Variaci%C3%B3n_de_entrop%C3%ADa_a_volumen_y_presi%C3%B3n_constante"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace