Campo eléctrico de un plano cargado GIA

De Laplace

Contenido 1 Enunciado 2 Solución 2.1 Campo eléctrico de un plano 2.1.1 Simetría del campo eléctrico

1 Enunciado

Sobre una superficie plana que puede considerarse infinita, se ha depositado una densidad superficial de carga uniforme, σ₀.

1. Calcúlese el campo eléctrico a ambos lados del plano.
2. Se dispone ahora otro plano, paralelo al anterior a una distancia d, y con una densidad superficial de carga uniforme − σ₀. Halle el campo eléctrico en todos los puntos del espacio.

2 Solución

2.1 Campo eléctrico de un plano

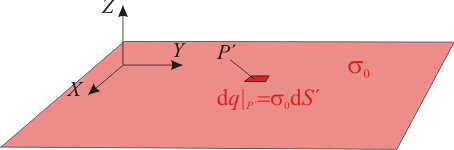
El plano infinito Π_f con una densidad superficial de carga eléctrica constante σ₀, es un modelo en primera aproximación del sistema consistente en una región plana de espesor despreciable, donde hay distribuida una cantidad de carga Q. Además, la región es lo suficientemente extensa como para poder considerar que, en puntos P' que se hallan lejos de la bordes, la carga se distribuye de manera uniforme, según la función densidad superficial de carga,

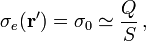
siendo S el área de la superficie cargada. En consecuencia, la validez del modelo y de los resultados que de él se deriven, se restringirá a la región del espacio que comprende puntos suficientemente alejados de los bordes de la superficie cargada, a la vez que tan próximos a ella como para que su tamaño pueda considerarse infinito.

Así pues, procedemos pues a calcular el campo eléctrico en puntos del espacio que pueden considerarse dentro del rango de validez del modelo de plano infinito Π_f con una distribución uniforme de carga, σ₀. Sin perder generalidad por ello, adoptaremos un sistema de coordenadas tal que el eje OZ sea perpendicular a dicho plano, de manera que Π_f:z = 0. Por otra parte, obsérvese que al admitir que tiene extensión infinita, el origen O del sistema de referencia podría ser cualquier punto del plano, de manera que las coordenadas x e y de los puntos del espacio se convierten en variables mudas que no aportan información alguna sobre la posición de cualquier punto en, o respecto del plano.

 

La distribución de carga uniforme e infinitamente extensa es simétrica respecto de cualquier plano vertical. Es de esperar, por tanto, que el campo eléctrico creado presente propiedades de simetría que permitan obtenerlo fácilmente mediante la aplicación de la ley de Gauss. En conscuencia, el primer paso será determinar las propieades geométricas de dicho campo

2.1.1 Simetría del campo eléctrico

Consideremos un punto P(z) que se encuentra a una distancia z sobre el plano cargado Π_f. En dicho plano podremos considerar infinitas circunferencias concéntricas, formadas cada una de de ellas por puntos que equidistan de P. Cada punto de cada una de las circunferencias constituye una carga puntual infinitesimal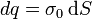 , que contribuirá con un 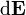al campo eléctrico total en el punto P. Al tratarse de una distrubición uniforme, habrá otra carga idéntica y diametralmente opuesta cuya contribución cancelerá la componente paralela al plano de la de su simétrica, mientras que duplica la componente en la dirección perpendicular (dirección “z”). Esto ocurrirá con todas las parejas de cargas simétricas que podemos considerar en todas y cada una de las circunferencias del plano Π_f, por lo que el campo eléctrico total en el punto P arbitrario, sólo va a tener componente en la dirección perpendicular al plano. Además, debido a la extensión infinita del plano, dicha componente sólo va a depender de la coordenada z del punto (es decir, de la distancia que lo separa de Π_f.

Pero obsérvese que en el punto P( − z), simétrico del anterior respecto del plano Π_f, la distribución de carga creará un campo eléctrico de igual dirección y magnitud que en el punto P(z), pero de sentido contrario. Y como el punto P(z) y su simétrico, P( − z),

es decir, a una distancia z por debajo del plano