Campo eléctrico de esfera cargada en su superficie GIA
De Laplace
1 Enunciado
Una carga Q se distribuye uniformemente en la superficie de una esfera de radio R. Calcule el campo eléctrico dentro y fuera de la esfera.
2 Solución
2.1 Esfera con carga distribuida en su superficie
Consideramos una esfera de radio R con una cantidad Qde carga eléctrica distribuida exclusivamente en su superficie. Este modelo puede responder tanto al caso de una esfera hueca de espesor despreciable (es decir, una superficie esférica Σf ) cargada, como al de una esfera maciza en la que todos los puntos interiores tienen carga neta nula, de manera que la densidad volumétrica de carga es cero.
La carga distribuida en la superficie estará descrita por la correspondiente densidad superficial de carga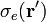 
. La uniformidad de la distribución indica que en todos los puntos P' de la superficie existirá la misma cantidad de carga por unidad de superficie, lo cuál es equivalente a que la relación entre la cantidad de carga contenida en un trozo arbitrario de superficie y el área de esta, debe ser constante. Si tomamos un sistema de referecia tal que su origen O coincida con el centro de la superficie esférica, ésta vendrá descrita por la ecuación,
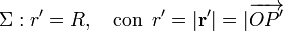
...y la densidad superficial de carga...
