Problemas de electrostática en el vacío

De Laplace

Contenido 1 Modelo semiclásico del átomo de Bohr 2 Electroscopio de dos hilos 3 Tres cargas en un triángulo equilátero 4 Cuatro cargas en un rectángulo 5 Tres cargas en un anillo 6 Fuerza entre dos hilos 7 Una esfera conductora rellena

1 Modelo semiclásico del átomo de Bohr

Supongamos un protón y un electrón situados a una distancia de un radio de Bohr

1. Calcule la fuerza eléctrica entre las dos partículas.
2. Halle la fuerza gravitatoria entre ellas.
3. Calcule el cociente entre las fuerza eléctrica y la gravitatoria.
4. Suponga que en lugar a una distancia de un radio de Bohr el protón se encuentra en el centro de la Tierra y el electrón en el centro de la Luna (a 384000 km), ¿cómo cambian las fuerzas eléctrica y gravitatoria? ¿Y el cociente entre ellas? De acuerdo con este resultado, ¿cómo se explica que la fuerza dominante en el sistema Tierra-Luna sea la gravedad?

2 Electroscopio de dos hilos

Un electroscopio mide la carga por la desviación angular de dos esferas idénticas conductoras, suspendidas por cuerdas aislantes de masas despreciables y longitud l. Cada esfera tiene una masa m y está sometida a la gravedad 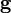. Las cargas pueden considerarse como puntuales e iguales entre sí. Halle la ecuación que liga el semiángulo θ con el valor de la carga total Q depositada en las esferas.

Suponga que la masa de cada esfera es 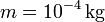y la longitud del cable del que penden es 20 cm. Admita asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1°. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?

3 Tres cargas en un triángulo equilátero

Tres cargas q₁, q₂ y q₃, se encuentran en los vértices de un triángulo equilátero de lado a = 1cm. Determine la fuerza sobre cada carga cuando:

1. .
2. .
3. , .
4. , .

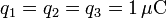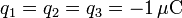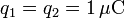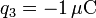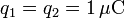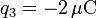4 Cuatro cargas en un rectángulo

Una carga puntual 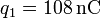se encuentra situada en el origen de coordenadas. En 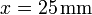, y = z = 0 se halla una segunda carga q₂. En 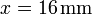, 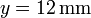se encuentra una tercera carga q₃.

Calcule el valor que deben tener q₂ y q₃ si, ocupando las´posiciones indicadas, se desea que sea nula la fuerza sobre una carga 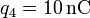situada en 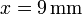, , 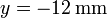z = 0.

5 Tres cargas en un anillo

Se dispone de tres cargas, una de valor Q y las otras dos de valor q. Estas cargas se ensartan en un anillo circular de radio R sobre el cual pueden deslizar libremente. Determine la ecuación para los ángulos del triángulo que forman las tres cargas. ¿Cuál es la solución para los casos 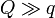, 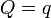y $?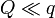

6 Fuerza entre dos hilos

Un cable formado por dos hilos paralelos produce un campo eléctrico similar al producido por dos líneas infinitas con densidad de carga λ y − λ, situadas a una distancia D una de la otra.

Se trata de hallar la fuerza por unidad de longitud con que se atraen los dos hilos. Para ello, calcule:

1. El campo eléctrico en cualquier punto del espacio, creado por un segmento rectilíneo de longitud L, sobre el cual existe una densidad de carga uniforme λ.
2. A partir del resultado anterior, halle el campo en cualquier punto debido a una línea de carga uniforme infinitamente larga.
3. Halle la fuerza que uno de los hilos produce sobre un segmento de longitud h del otro hilo.

7 Una esfera conductora rellena

Una superficie esférica conductora de radio R, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma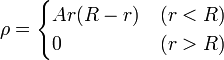

1. Calcule el campo eléctrico en todos los puntos del espacio.
2. Calcule el valor de la carga almacenada en la esfera conductora.
3. Halle el potencial eléctrico en el centro de la esfera.
   1. A partir del campo eléctrico.
   2. Por integración directa a partir de las densidades de carga.
4. Halle la energía electrostática almacenada en el sistema.