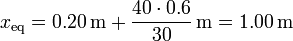Entrar Página Discusión Historial Go to the site toolbox

Masa con resorte en plano inclinado

De Laplace

Contenido

1 Enunciado

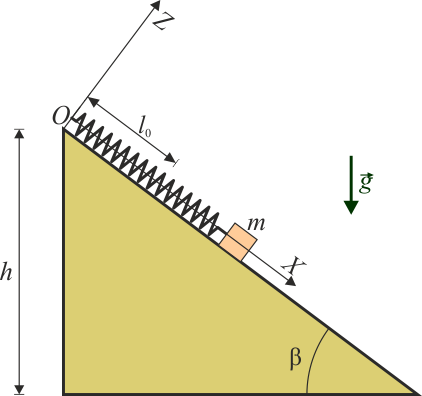
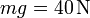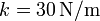Un bloque de peso mg=40\,\mathrm{N} se encuentra sobre un plano inclinado de altura h=1.2\,\mathrm{m} y pendiente del 75%. El bloque se encuentra atado al punto superior del plano por un resorte de constante k=30\,\mathrm{N}/\mathrm{m} y longitud natural 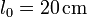l_0=20\,\mathrm{cm}. Para hacer el estudio se considera el sistema de ejes indicado en la figura.

  1. Suponiendo que no existe rozamiento entre el bloque y el plano, determine la distancia xeq a la que la masa se queda en equilibrio.
  2. Suponga que inicialmente el bloque se encuentra sujeto a una distancia igual a la longitud natural del resorte y en ese momento se suelta. ¿Cuánto vale su rapidez cuando pasa por la distancia de equilibrio xeq? ¿Cuál es la distancia máxima xmax a la que llega el bloque?
  3. Suponga ahora que existe un coeficiente de rozamiento estático μ = 0.25 entre el bloque y el plano. ¿Entre qué valores de x puede situarse la masa en reposo, quedándose en equilibrio?
Archivo:masa-plano-resorte.png

2 Posición de equilibrio

La posición de equilibrio será aquella en la que la suma de fuerzas sobre la masa sea cero. En ausencia de rozamiento tenemos tres fuerzas actuando sobre el bloque: el peso, la fuerza elástica y la reacción normal del plano

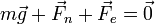
m\vec{g}+\vec{F}_n+\vec{F}_e=\vec{0}

Empleando el sistema de ejes indicado en el enunciado, cada una de estas fuerzas se escribe:

Peso
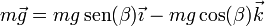
m\vec{g} = mg\,\mathrm{sen}(\beta)\vec{\imath}-mg\cos(\beta)\vec{k}
Fuerza normal
Esta va en la dirección del eje OZ positivo
\vec{F}_n = F_n\vec{k}
Fuerza elástica
Es tangente al plano inclinado y proporcional a la diferencia entre la elongación y la longitud natural
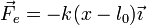
\vec{F}_e =-k(x-l_0)\vec{\imath}

Sumando los tres vectores y separando por componentes

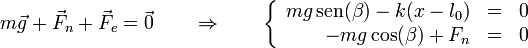
m\vec{g}+\vec{F}_n+\vec{F}_e=\vec{0}\qquad\Rightarrow\qquad \left\{\begin{array}{rcl} mg\,\mathrm{sen}(\beta)-k(x-l_0)&=& 0 \\ -mg\cos(\beta)+F_n & = & 0 \end{array}\right.

lo que nos da la posición de equilibrio

x_\mathrm{eq} = l_0+\frac{mg\,\mathrm{sen}(\beta)}{k}

donde, en este caso

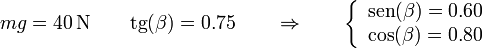
mg = 40\,\mathrm{N}\qquad\mathrm{tg}(\beta)=0.75\qquad\Rightarrow\qquad\left\{\begin{array}{c} \mathrm{sen}(\beta) = 0.60 \\ \cos(\beta) = 0.80\end{array}\right.

y queda la distancia

x_\mathrm{eq}=0.20\,\mathrm{m}+\frac{40\cdot 0.6}{30}\,\mathrm{m}=1.00\,\mathrm{m}

3 Rapidez y alcance máximos

4 Zona de equilibrio

Obtenido de "http://tesla.us.es/wiki/index.php/Masa_con_resorte_en_plano_inclinado"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace