Masa con resorte en plano inclinado
De Laplace
Contenido |
1 Enunciado
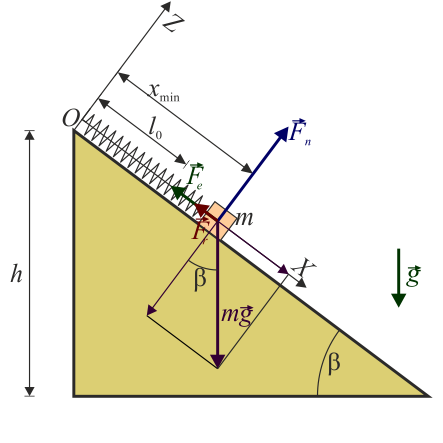
Un bloque de peso 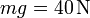 se encuentra sobre un plano inclinado de altura
se encuentra sobre un plano inclinado de altura  y pendiente del 75%. El bloque se encuentra atado al punto superior del plano por un resorte de constante
y pendiente del 75%. El bloque se encuentra atado al punto superior del plano por un resorte de constante 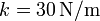 y longitud natural
y longitud natural 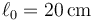 . Para hacer el estudio se considera el sistema de ejes indicado en la figura.
. Para hacer el estudio se considera el sistema de ejes indicado en la figura.
- Suponiendo que no existe rozamiento entre el bloque y el plano, determine la distancia
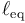 a la que la masa se queda en equilibrio.
a la que la masa se queda en equilibrio.
- Suponga que inicialmente el bloque se encuentra sujeto a una distancia igual a la longitud natural del resorte y en ese momento se suelta. ¿Cuánto vale su rapidez cuando pasa por la distancia de equilibrio
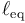 ? ¿Cuál es la distancia máxima
? ¿Cuál es la distancia máxima 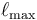 a la que llega el bloque?
a la que llega el bloque?
- Suponga ahora que existe un coeficiente de rozamiento estático μ = 0.25 entre el bloque y el plano. ¿Entre qué valores de
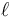 puede situarse la masa en reposo, quedándose en equilibrio?
puede situarse la masa en reposo, quedándose en equilibrio?
2 Posición de equilibrio
La posición de equilibrio será aquella en la que la suma de fuerzas sobre la masa sea cero. En ausencia de rozamiento tenemos tres fuerzas actuando sobre el bloque: el peso, la fuerza elástica y la reacción normal del plano
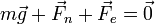
Empleando el sistema de ejes indicado en el enunciado, cada una de estas fuerzas se escribe:
- Peso
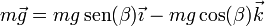
- Fuerza normal
- Esta va en la dirección del eje OZ positivo

- Fuerza elástica
- Es tangente al plano inclinado y proporcional a la diferencia entre la longitud instantánea y la longitud natural

Sumando los tres vectores y separando por componentes
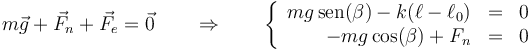
lo que nos da la longitud de equilibrio

donde, en este caso
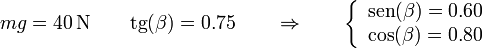
y queda la distancia
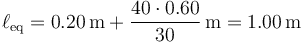
Obsérvese que la longitud de equilibrio no coincide con la longitud natural, sino que es mayor que esta, ya que la el peso estira el muelle.
3 Rapidez y alcance máximos
Cuando la partícula se suelta desde un punto que no sea la posición de equilibrio, describe un movimiento armónico simple alrededor de esta posición.
Las fuerzas que actúan sobre la masa son las mismas que antes, pero ya no se anulan mutuamente
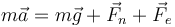
Separando por componentes

La fuerza normal sigue compensando a la componente normal del peso
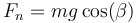
Para estudiar la componente paralela al plano definimos la elongación del muelle como la diferencia respecto a la posición de equilibrio (que no la longitud natural)
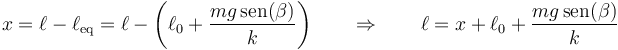
Empleando la elongación, la ley de Newton queda
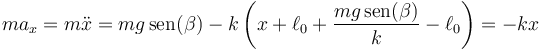
Esto es la ecuación de un oscilador armónico en torno a la posición de equilibrio x = 0. Obsérvese como con este cambio de variables el peso desaparece aparentemente de las ecuaciones y no tenemos que añadir el correspondiente término
La energía potencial asociada a la fuerza que mueve a la masa es la correspondiente a un oscilador armónico
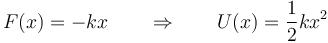
3.1 Alcance máximo
Si la partícula se encuentra en la posición inicial igual a la longitud natural,
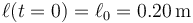
su elongación inicial es la diferencia entre esta y la longitud de equilibrio
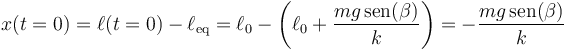
Numéricamente
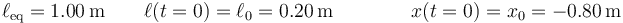
Una vez que se suelta, la partícula describe oscilaciones alrededor del punto de equilibrio. Puesto que parte del reposo, la amplitud de las oscilaciones es igual a la diferencia entre la posición de equilibrio y la inicial

El alcance máximo se obtiene cuando la masa llega a una distancia igual a la amplitud por el otro lado del punto de equilibrio
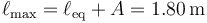
3.2 Rapidez máxima
La rapidez máxima se alcanza cuando el bloque pasa por la posición de equilibrio. En este momento la energía potencial elástica se ha transformado en energía cinética, cumpliéndose la igualdad
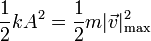
lo que nos da la rapidez máxima
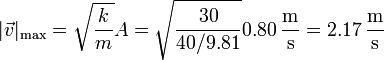
3.3 Solución alternativa
Una forma alternativa más larga de llegar a estos mismos resultados consiste en considerar por separado la energía potencial gravitatoria y la elástica, de manera que
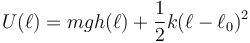
La altura puede medirse desde cualquier nivel de referencia, no necesariamente desde el punto más bajo del plano. Si optamos por medirlo desde este punto, la altura para cada valor de 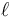 será, en metros,
será, en metros,
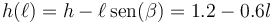
La altura inicial es, de acuerdo con esta fórmula
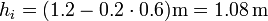
y en la posición de equilibrio
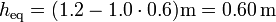
La conservación de la energía mecánica nos da, para el cálculo de la rapidez máxima
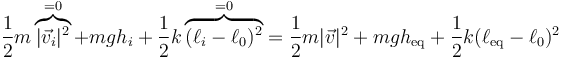
En forma numérica, midiendo la energía en julios
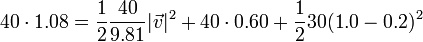
Despejando de aquí

El alcance máximo se obtiene de la misma forma, buscando en qué punto la energía cinética vuelve a ser nula.
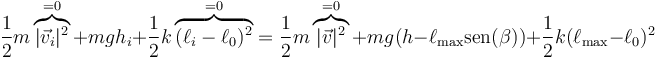
Esto nos da la ecuación de segundo grado, con todas las magnitudes en el SI
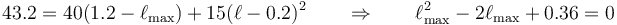
Las dos soluciones de esta ecuación son 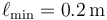 , correspondiente a la posición inicial y
, correspondiente a la posición inicial y
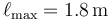
Como se ve, este método desarrollado conduce a la solución correcta pero es mucho más largo y proclive a errores que el anterior.
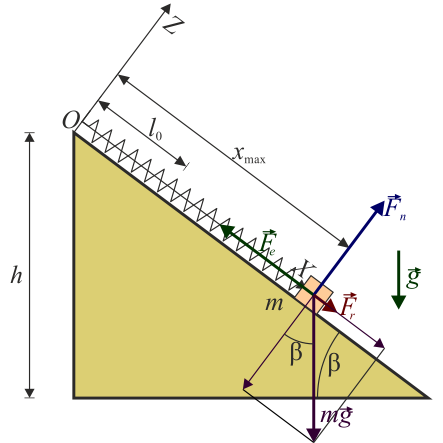
4 Zona de equilibrio
Cuando tenemos fricción entre el bloque y el plano, además de las tres fuerzas del primer apartado, tenemos también que añadir la fuerza de rozamiento. Esta fuerza es tangente a la superficie
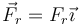
lo que nos da las ecuaciones de equilibrio
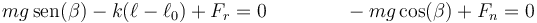
En la posición de equilibrio del primer apartado, la fuerza de rozamiento es nula ya que la fuerza elástica compensa al peso y no se ejerce fuerza externa sobre el bloque. Si se separa de esta posición, la fuerza de rozamiento va aumentando, hasta que llega a su valor límite. A partir de ahí no es capaz de compensar la diferencia entre la fuerza elástica y el peso, y el bloque se mueve. El valor máximo de la fuerza de rozamiento lo da la condición de deslizamiento inminente
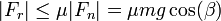
con lo que los valores extremos de la posición los da el que se alcance la igualdad, esto es, cuando
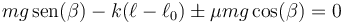
lo que da las posiciones extremas
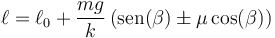
Sustituyendo los valores numéricos
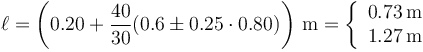
Por tanto, la masa se quedará en reposo si
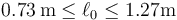
En un extremo la fuerza de rozamiento irá en un sentido y en el otro apuntará en el sentido opuesto.