Equilibrio de una barra apoyada
De Laplace
Contenido |
1 Enunciado
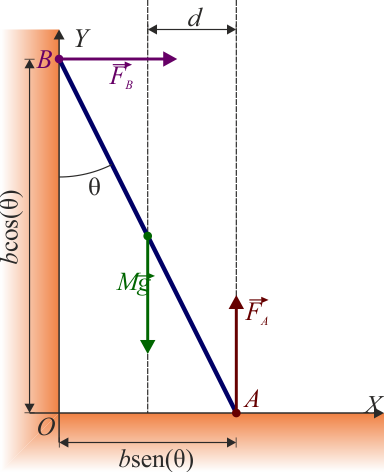
Supongamos que tenemos una barra de masa M y longitud H apoyada en el suelo y en una pared vertical.
- Suponga primero que no hay rozamiento con las superficies y que la barra forma un ángulo θ con la vertical. ¿Puede quedarse en equilibrio la barra para algún valor de θ?
- Suponga ahora que la barra posee un coeficiente de rozamiento estático μ con el suelo. ¿Para qué ángulos puede alcanzarse entonces el equilibrio?
2 Sin rozamiento
La condición para que un sólido esté en equilibrio es que la fuerza resultante y el momento resultante (respecto de cualquier punto) sean nulos.

En este sistema tenemos tres fuerzas actuando sobre la barra
- Su peso,
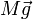
- La reacción del suelo,
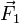
- La reacción de la pared,
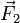
En principio, el peso de la barra no es una sola fuerza, sino una infinitud de ellas (cada trocito de barra tiene su propio peso). Lo que ocurre es que este sistema de infinitas fuerzas diferenciales es equivalente a una sola fuerza de valor el peso total y aplicada en el centro de gravedad del sólido.
Si situamos el origen de coordenadas en la esquina, el valor del peso y su punto de aplicación son

La reacción del suelo se aplica en el punto de contacto de la barra con él. Por ser una superficie sin rozamiento, su dirección es puramente normal al suelo. Por ser un vínculo unilateral, su sentido es necesariamente hacia afuera del suelo

La reacción de la pared se aplica en el punto de apoyo en ella, su dirección es también perpendicular y su sentido es hacia afuera
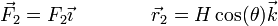
La condición de equilibrio es e, primer lugar, que la suma de fuerzas sea igual a cero
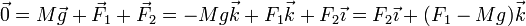
lo cual implica, separando por componentes,

es decir, la reacción del suelo debe compensar al peso, mientras que la de la pared no tiene que compensar a nadie, por lo que es nula.
No basta con que la resultante sea nula, también debe serlo el momento resultante. Para que se anule el momento, podemos tomar cualquier punto como referencia. Considerando el momento respecto al punto O, la esquina de la pared con el suelo, debe ser
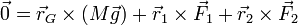
Sustituyendo cada una de las posiciones y fuerzas