Sistemas simples de sólidos rígidos
De Laplace
Contenido |
1 Introducción
Las aplicaciones de la dinámica del sólido rígido son incalculables ya que gran parte de la teoría de máquinas y mecanismos puede realizarse suponiendo que los distintos componentes son aproximadamente rígidos. La mayoría de estas aplicaciones, incluso las de apariencia sencilla, no obstante, suele implicar complejos cálculos matemáticos, por lo que escapan al alcance de esta introducción.
2 Estática del sólido
La estática del sólido (y de los sistemas de sólidos) es el estudio de las condiciones en que un sólido o sistema permanece en reposo. Matemáticamente la expresión de la condición de equilibrio es muy simple:

Sin embargo, la aplicación práctica de estas ecuaciones es mucho más complicada, ya que a menudo una o varias de las fuerzas que actúan sobre el sólido son fuerzas de reacción vincular, cuyo valor es desconocido a priori y que son incógnitas adicionales del problema. Normalmente, un problema de estática de sólidos se compone de varios elementos:
- Determinación de la(s) posición(es) de equilibrio posibles, si existen.
- Cálculo de las fuerzas y pares de reacción vincular.
Adicionalmente, suele existir una parte que requiere el estudio de la energía del sistema y del comportamiento de éste cuando se somete a una perturbación:
- Determinación de la estabilidad de los puntos de equilibrio.
Como ejemplo sencillo, tenemos el estudio del equilibrio de una barra apoyada en el suelo y en una pared.
3 Movimiento de un sólido libre
Cuando sobre un sólido la resultante de las fuerzas y el momento resultante se anulan

ello no implica que el sólido esté necesariamente en reposo, solo que no se ve acelerado. El estado de reposo es solo un caso particular.
En general, lo que podemos afirmar es que la cantidad de movimiento y el momento cinético permanecen constantes

Estas dos ecuaciones implican que también se conserva el momento cinético respecto al centro de masas
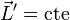
y puesto que la potencia desarrollada sobre el sólido es nula también se conserva su energía cinética

De la conservación de la cantidad de movimiento se deduce que el centro de masas se mueve con un movimiento rectilíneo y uniforme.
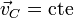
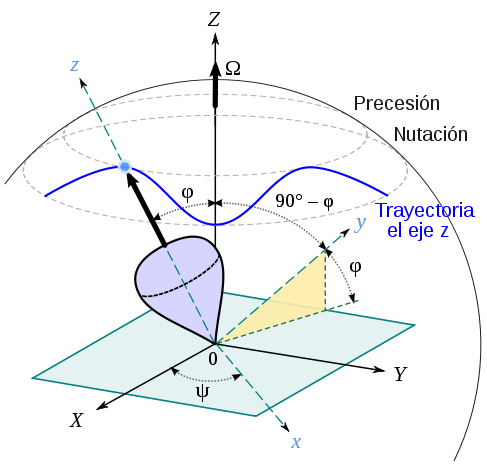
La analogía entre traslación y rotación nos sugiere que la conservación del momento cinético implica que la velocidad angular es constante, pero esto no es cierto en general. Lo más que podemos afirmar en general es que la componente de la velocidad angular en la dirección del momento cinético sí permanece constante. Pero las componentes en otras direcciones pueden variar. El sólido puede desarrollar un movimiento de precesión en el cual el sólido gira en torno a un eje instantáneo de rotación, que está rotando a su vez.
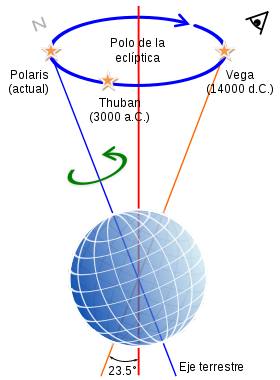
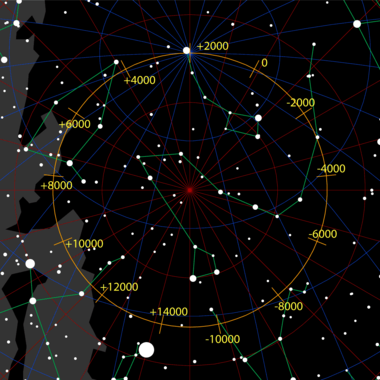
Así, por ejemplo, la Tierra es un sólido aproximadamente libre en cuanto a su rotación (no en la traslación, gobernada por la fuerza gravitatoria) y su eje desarrolla un movimiento de precesión que provoca que la estrella situada en el polo norte celeste vaya cambiando. Hoy día es la Estrella Polar, pero hace 16000 años era la estrella Vega.
En el caso de un sólido simétrico, como una esfera perfecta o un cubo, en el que la velocidad angular es paralela al momento cinético, la conservación del segundo implica la constancia de la primera

Incluso en el caso de que la velocidad del CM y la velocidad angular permanezcan constantes, el movimiento de los partículas de un sólido libre puede ser muy complicado. Así, por ejemplo, en el caso de un sólido formado por dos partículas unidas por una barra, el movimiento de cada una puede ser una cicloide

4 Giróscopo
Un giróscopo consiste esencialmente en un sólido que, por su elevado momento de inercia y su gran velocidad de giro posee un momento cinético de gran magnitud
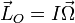
Lo que hace especial a este sólido es que un par de fuerzas aplicado sobre él apenas modifica la dirección de su eje de rotación. Por ejemplo, supongamos un disco pesado rotando alrededor del eje Z, con momento cinético respecto a su centro

Supongamos que sobre este disco rotatorio se ejerce un par de fuerzas, de forma que se empuja el eje de giro a una altura h por encima del disco con una fuerza 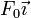 y a una distancia h por debajo una fuerza
y a una distancia h por debajo una fuerza 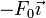 . ¿Hacia dónde se inclina el disco?
. ¿Hacia dónde se inclina el disco?
Un análisis ingenuo sugeriría que gira alrededor del eje OY, pero no es así. El momento del par aplicado vale
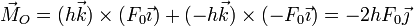
luego aparece una aceleración angular en la dirección del eje OY, pero esto no quiere decir que rote alrededor de este eje, ya que el disco ya poseía una cierta velocidad angular. Lo que nos da el par es la variación del momento cinético

En forma vectorial
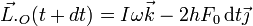
Esto nos da la nueva velocidad angular
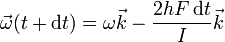
La velocidad angular es la que da el eje de giro, por lo que vemos que este eje (perpendicular al disco) adquiere una componente en la dirección del eje OY, esto es, gira en torno al eje OX (¡perpendicularmente a como diría la intuición!). Además este giro es muy pequeño, ya que el ángulo que la nueva velocidad angular forma con el eje OZ cumple
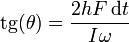
con lo cual, dado que el disco dispone de un elevado momento cinético inicial, el denominador será muy grande y el ángulo correspondiente será minúsculo. Idealmente, se supone un momento cinético infinito, con lo que es imposible variar el eje de giro. De esta forma, un giróscopo mantendría su orientación en cualquier circunstancia, sirviendo como elemento orientador, al estilo de una brújula.
Un giróscopo comercial se monta sobre un armazón consistente en una junta cardán que le permite girar manteniendo su eje siempre en la misma dirección, aunque el armazón se encuentre montado en un soporte móvil (un barco o un avión)

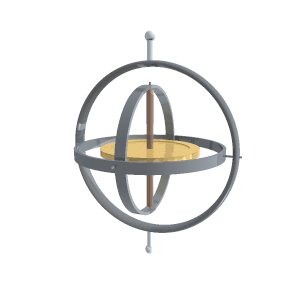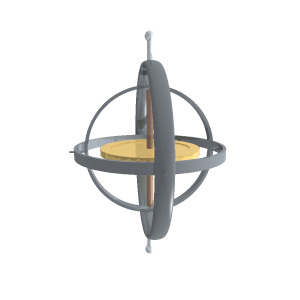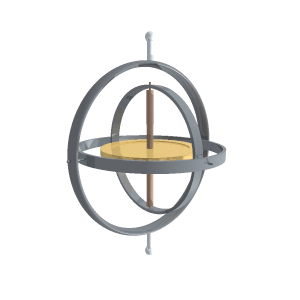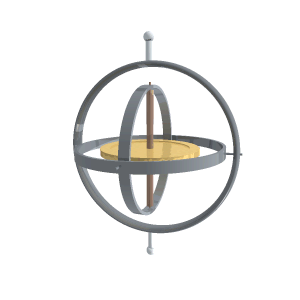
5 Ley de la palanca
La ley de la palanca es una aplicación clásica de la dinámica de sólidos rígidos, conocida desde la antigüedad.
En su versión más simple consiste en una palanca (una plataforma, por ejemplo) apoyada sobre un punto (el fulcro) en torno al cual puede girar.

A un lado del fulcro y a una distancia b1 de él se aplica una fuerza 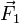 (denominada, por razones históricas, la potencia). A una distancia b2 del fulcro se encuentra una carga que ejerce una fuerza
(denominada, por razones históricas, la potencia). A una distancia b2 del fulcro se encuentra una carga que ejerce una fuerza 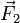 (la resistencia), que debe vencerse con ayuda de la palanca. La pregunta es ¿cuál es la mínima potencia que debe aplicarse para vencer una resistencia dada?
(la resistencia), que debe vencerse con ayuda de la palanca. La pregunta es ¿cuál es la mínima potencia que debe aplicarse para vencer una resistencia dada?
La potencia mínima es aquella que consigue equilibrar la palanca, lo cual implica que el momento respecto al fulcro es nulo
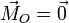
Tomando como eje OX el tangente a la palanca y con origen en el fulcro, el momento tal vale
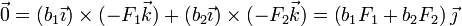
de donde obtenemos la relación
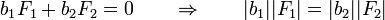
que se enuncia como el producto de la potencia por su brazo es igual al de la resistencia por el suyo (ley de la palanca). Técnicamente ns dice que el par ejercido por una de las fuerzas sobre la palanca debe compensar el ejercido por la otra.
Por la tercera ley de Newton, si la resistencia ejerce una fuerza 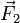 sobre la palanca, ésta ejerce una fuerza
sobre la palanca, ésta ejerce una fuerza 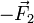 sobre la carga. Esto nos dice que en una situación de equilibrio, al ejercer una fuerza
sobre la carga. Esto nos dice que en una situación de equilibrio, al ejercer una fuerza 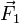 en la posición de la potencia se transmite una fuerza
en la posición de la potencia se transmite una fuerza 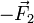 en la posición de la resistencia. Esta segunda fuerza podrá ser mayor o menor que la primera, dependiendo de la longitud de los respectivos brazos.
en la posición de la resistencia. Esta segunda fuerza podrá ser mayor o menor que la primera, dependiendo de la longitud de los respectivos brazos.
Por sus aplicaciones técnicas, las palancas se califican en tres tipos:
- Palanca de primera especie
- Es la que tiene la potencia a un lado del fulcro y la resistencia al otro (b1 < 0, b2 > 0.

- Una potencia hacia abajo resulta en un empuje hacia arriba en la resistencia. La magnitud de la fuerza sobre la resistencia es
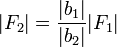
- Si | b1 | > | b2 | la fuerza transmitida a la resistencia es superior a la ejercida sobre la potencia. Eligiendo el brazo de la potencia lo largo que sea necesario es posible vencer (teóricamente) cualquier resistencia y levantar cualquier objeto.
- Palanca de segunda especie
- Es aquella en la que la resistencia se encuentra entre la potencia y el fulcro.

- En ella la fuerza sobre la resistencia va en el mismo sentido que la potencia ejercida, pero es de mayor magnitud (ya que necesariamente b2 < b1. Ejemplos de palancas de segunda especie serían el cascanueces o los remos de una piragua (cuyo punto de apoyo es el agua).
- Palanca de tercera especie
- Es aquella en la que la potencia se encuentre entre la resistencia y el fulcro.
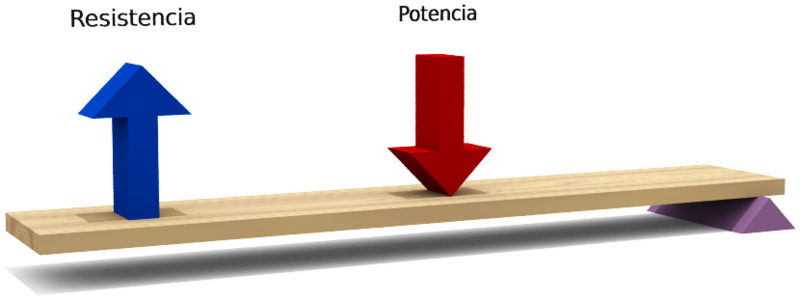
- En ella la fuerza sobre la resistencia va en el mismo sentido que la potencia ejercida, siendo ahora de menor magnitud (ya que b2 > b1. Una palanca de tercera especie interesa cuando se desea multiplicar el desplazamiento de la carga o su velocidad. Un ejemplo de palanca de tercera especie es la mandíbula humana.
Tanto en la palanca de primera especie cuando | b2 | < | b1 | como en la de segunda especie, la resistencia que se vence es superior a la potencia. Con ayuda de una palanca seríamos capaces de levantar un piano de cola simplemente apretando con el pulgar, o de romper una barra de acero con un cascanueces.
Parece que esto violaría alguna ley de conservación, pues estaríamos obteniendo fuerza “gratis”. La clave es la respuesta a la pregunta ¿cuánto levantaríamos el piano? Si empujando en la potencia realizamos un desplazamiento dz1 esto quiere decir que la palanca gira un ángulo
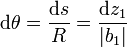
Este giro se traduce en una elevación en la resistencia
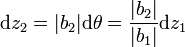
es decir, el desplazamiento en la resistencia será menor que el de la potencia. El trabajo realizado sobre la resistencia es igual a
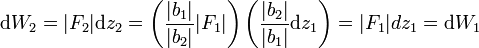
con lo que el trabajo que se realiza por un lado es el que se saca por el otro, por lo que no se viola la ley de conservación de la energía.
6 Vuelco inminente
7 Movimiento de una peonza pesada