Electrostática en presencia de conductores
De Laplace
1 Equilibrio electrostático
La propiedad definitoria de un material conductor es que permite el movimiento de las cargas en su interior. Cuando un conductor se ve sometido a un campo eléctrico, las cargas se redistribuyen hasta que se alcanza el equilibrio electrostático, en el cual las cargas se encuentran en reposo.
La condición de reposo implica que la fuerza neta sobre cada carga es nula. Puesto que la fuerza sobre las cargas en reposo es una fuerza eléctrica, la condición de equilibrio implica que en el material conductor
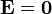
2 Propiedades de los conductores en equilibrio
Como consecuencia de la condición de equilibrio electrostático
- El material conductor es equipotencial.
- No hay densidad de carga de volumen en el material.
- Toda la carga está almacenada en las superficies del conductor.
- No hay líneas de campo que vayan de un conductor a él mismo.
- El campo justo en el exterior de la superficie es de la forma
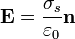
3 Problema del potencial
Si tenemos un conjunto de conductores cuya carga o cuyo potencial es conocido, además de una cierta distribución de carga volumétrica en el espacio entre ellos, el problema del potencial consiste en resolver la ecuación de Poisson
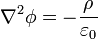
en el espacio τ entre los conductores, con las condiciones de contorno
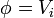
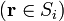
siendo Si la superficie del conductor i. Para aquellos conductores cuyo potencial no se conozca, sus valores pueden obtenerse de las condiciones
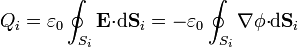
siendo Si una superficie que envuelve al conductor i.
La solución del problema del potencial puede escribirse como una superposición
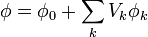
siendo φ0 el potencial que habría si la densidad de carga estuviera presente pero los conductores estuvieran a tierra
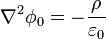
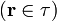 φ0 = 0
φ0 = 0 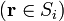
y φk es el potencial supuesto que el conductor k está a potencial unidad y el resto a tierra
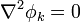
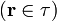
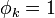
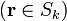
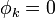
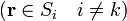
4 Coeficientes de capacidad
Si no hay densidad de carga volumétrica, las cargas almacenadas en los distintos conductores forman una combinación lineal de los potenciales respectivos
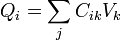
siendo los Cik los coeficientes de capacidad.
Estas relaciones pueden expresarse en forma matricial
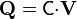
siendo 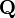 y
y 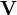 dos vectores columna y
dos vectores columna y 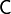 una matriz cuadrada simétrica y definida positiva.
una matriz cuadrada simétrica y definida positiva.
Los coeficientes de capacidad verifican
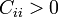
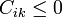
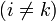
4.1 Capacidad de un conductor
En el caso particular de un solo conductor, la expresión se reduce a
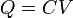
con C la capacidad del conductor, medida en faradios (F). Como caso particular, para una esfera de radio R
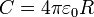
5 Condensadores y circuitos equivalentes
6 Método de las imágenes
7 Métodos numéricos
8 Energía de un sistema de conductores
9 Presión sobre la superficie de los conductores
10 Fuerzas entre conductores
11 Problemas
Artículo completo: Problemas de campo eléctrico en presencia de conductores





