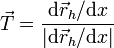Entrar Página Discusión Historial Go to the site toolbox

Triedro intínseco de una hipérbola, Noviembre 2011 (G.I.C.)

De Laplace

Revisión a fecha de 12:27 18 nov 2011; Pedro (Discusión | contribuciones)
(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Se tiene la hipérbola de la figura, que viene dada por la ecuación y = C2 / x, siendo C una constante.

  1. ¿Cuál de las siguientes expresiones corresponde al vector tangente en cada punto?
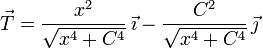    1. \vec{T}=\dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\imath} - \dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
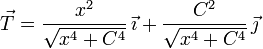    2. \vec{T}=\dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\imath} + \dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
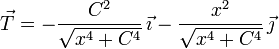    3. \vec{T}=-\dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\imath} - \dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
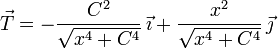    4. \vec{T}=-\dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\imath} + \dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
  2. ¿Cuál de las siguientes expresiones corresponde al vector normal en cada punto?
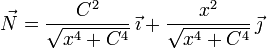    1. \vec{N}=\dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\imath} + \dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
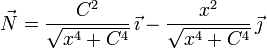    2. \vec{N}=\dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\imath} - \dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
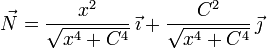    3. \vec{N}=\dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\imath} + \dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
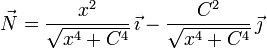    4. \vec{N}=\dfrac{x^2}{\sqrt{x^4+C^4}}\,\vec{\imath} - \dfrac{C^2}{\sqrt{x^4+C^4}}\,\vec{\jmath}.
  3. Un punto recorre la hipérbola de modo que la coordenada sobre el eje X depende del tiempo como 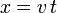x=v\,t (suponemos t > 0). La aceleración tangencial en un instante de tiempo t es
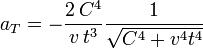    1. a_T=-\dfrac{2\,C^4}{v\,t^3}\dfrac{1}{\sqrt{C^4+v^4t^4}}.
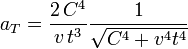    2. a_T=\dfrac{2\,C^4}{v\,t^3}\dfrac{1}{\sqrt{C^4+v^4t^4}}.
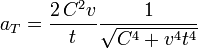    3. a_T=\dfrac{2\,C^2v}{t}\dfrac{1}{\sqrt{C^4+v^4t^4}}.
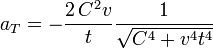    4. a_T=-\dfrac{2\,C^2v}{t}\dfrac{1}{\sqrt{C^4+v^4t^4}}.


2 Solución

2.1 Vector tangente

El vector de posición de un punto genérico en el plano es

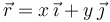
\vec{r}= x\,\vec{\imath} + y\,\vec{\jmath}

Si imponemos que ese punto esté sobre la hipérbola las componentes x e y están relacionadas por la ecuación de la hipérbola. El vector de posición de un punto situado en la curva es

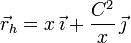
\vec{r}_h = x\,\vec{\imath} + \dfrac{C^2}{x}\,\vec{\jmath}

El vector tangente es

\vec{T} = \dfrac{\mathrm{d}\vec{r}_h/\mathrm{d}x}{|\mathrm{d}\vec{r}_h/\mathrm{d}x|}

Obtenido de "http://tesla.us.es/wiki/index.php/Triedro_int%C3%ADnseco_de_una_hip%C3%A9rbola,_Noviembre_2011_(G.I.C.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace