Movimiento oscilatorio circular
De Laplace
Revisión a fecha de 18:32 13 nov 2011; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Una partícula se mueve sobre la circunferencia, expresada en polares y en el SI, 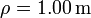 , siguiendo la ley horaria
, siguiendo la ley horaria
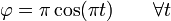
con  el ángulo que el vector de posición forma con el eje OX positivo.
el ángulo que el vector de posición forma con el eje OX positivo.
- Determine la aceleración angular en t = (1 / 3)s
- Halle la velocidad lineal cuando pasa por
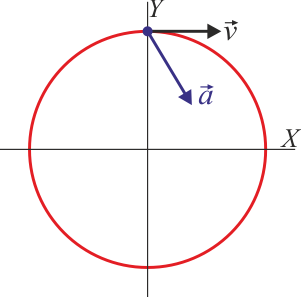
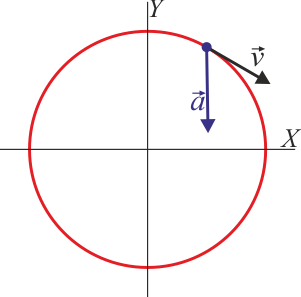
- Indique cuál de las siguientes cuatro figuras corresponde a la velocidad y la aceleración en t = (1 / 3)s
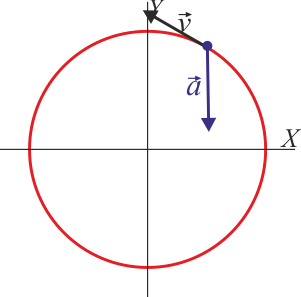
| 
|
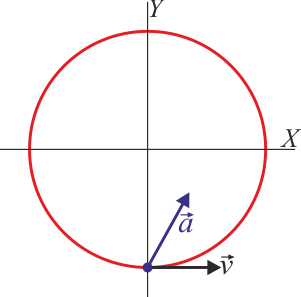
| 
|





