Parámetro arco de una hélice (G.I.A.)

De Laplace

Revisión a fecha de 16:16 25 oct 2011; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

Sea la hélice $Γ$ descrita en un sistema de referencia cartesiano $O X Y Z$ por las siguientes ecuaciones paramétricas:

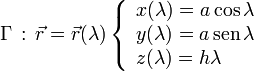
$\Gamma\,:\,\vec{r} = \vec{r}(\lambda) \left\{ \begin{array}{l} x(\lambda) = a \cos\lambda\\ y(\lambda) = a \,\mathrm{sen}\,\lambda\\ z(\lambda) = h \lambda \end{array} \right.$

donde $a$ y $h$ son constantes conocidas.

Determina la longitud recorrida sobre la hélice (parámetro arco) en función del parámetro $λ$ .
Obtén los vectores del triedro intrínseco en cada punto de dicha curva.
Calcula su radio de curvatura.

2 Solución

2.1 Distancia recorrida

Podemos calcular la distancia recorrida sobre la hélice sumando los módulos de los 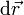$\mathrm{d}\vec{r}$ obtenidos al variar el parámetro una cantidad infinitesimal $dλ$ . La expresión de 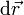$\mathrm{d}\vec{r}$ es

$\mathrm{d}\vec{r} = \left(\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right)\,\mathrm{d}\lambda$

Derivando el vector tenemos

$\left(\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right) = -a\cos\lambda\,\vec{\imath} + +a\,\mathrm{sen}\,\lambda\,\vec{\jmath} + h\,\vec{k}$

La distancia recorrida en este paso infinitesimal es

$\mathrm{d}s=|\mathrm{d}\vec{r}|=\left|\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right| \,\mathrm{d}\lambda = \mathrm{d}\lambda\,\sqrt{a^2\cos^2\lambda + a^2\mathrm{sen}^2\lambda + h^2} = \mathrm{d}\lambda\,\sqrt{a^2+h^2}$

Si empezamos a contar la distancia recorrida en $λ = 0$ la distancia para un valor de $λ$ es

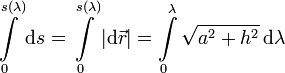
$\int\limits_{0}^{s(\lambda)}\mathrm{d}s = \int\limits_{0}^{s(\lambda)}|\mathrm{d}\vec{r}| = \int\limits_0^{\lambda}\sqrt{a^2+h^2}\,\mathrm{d}\lambda$

Integrando obtenemos

$s(\lambda) = \lambda\,\sqrt{a^2+h^2}$

La distancia recorrida sobre la curva recibe el nombre de parámetro arco. Puede utilizarse también para parametrizar la curva.

2.2 Triedro intrínseco

Calculamos el triedro intrínseco en cada punto de la curva usando las expresiones que dependen sólo de la parametrización de la curva, no de las variables cinemáticas ( velocidad y aceleración ).

El vector tangente es

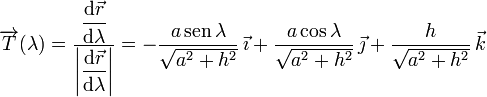
$\overrightarrow{T}(\lambda) = \dfrac{\displaystyle\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}}{\displaystyle\left|\dfrac{\mathrm{d}\vec{r}}{\mathrm{d}\lambda}\right|} = -\dfrac{a\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath} + \dfrac{a\cos\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath} + \dfrac{h}{\sqrt{a^2+h^2}}\,\vec{k}$

El vector normal se define en términos de la derivada del vector tangente respecto al parámetro.

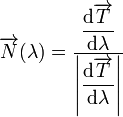
$\overrightarrow{N}(\lambda) = \dfrac{\displaystyle\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}}{\displaystyle\left|\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}\right|}$

Derivando el vector tangente

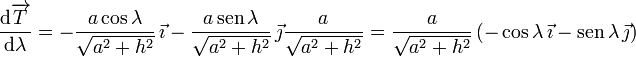
$\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}= -\dfrac{a\cos\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath} - \dfrac{a\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\jmath} \dfrac{a}{\sqrt{a^2+h^2}} = \dfrac{a}{\sqrt{a^2+h^2}} \left(-\cos\lambda\,\vec{\imath} - \mathrm{sen}\,\lambda\,\vec{\jmath}\right)$

El módulo de este vector es

$\left|\dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda}\right| =\dfrac{a}{\sqrt{a^2+h^2}}$

Y el vector normal es

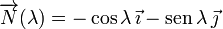
$\overrightarrow{N}(\lambda) = -\cos\lambda\,\vec{\imath} - \mathrm{sen}\,\lambda\,\vec{\jmath}$

El vector binormal se define como

$\overrightarrow{B}(\lambda) = \overrightarrow{T}\times\overrightarrow{N} = \dfrac{h\,\mathrm{sen}\,\lambda}{\sqrt{a^2+h^2}}\,\vec{\imath}- \dfrac{h\,\mathrm{cos}\,\lambda}{\sqrt{a^2+h^2}a}\,\vec{\jmath} +\dfrac{a}{\sqrt{a^2+h^2}}\,\vec{k}$

2.3 Curvatura

La curvatura es el módulo de la derivada del vector tangente, cuando este está expresado en términos del parámetro arco. Esto es

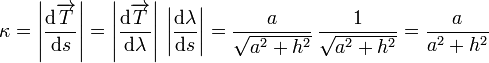
$\kappa = \left| \dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}s} \right| = \left| \dfrac{\mathrm{d}\overrightarrow{T}}{\mathrm{d}\lambda} \right| \,\left|\dfrac{\mathrm{d}\lambda}{\mathrm{d}s} \right| = \dfrac{a}{\sqrt{a^2+h^2}}\,\dfrac{1}{\sqrt{a^2+h^2}} = \dfrac{a}{a^2+h^2}$

Y el radio de curvatura es

$R_{\kappa} = \dfrac{1}{\kappa} = \dfrac{{a^2+h^2}}{a}$

Parámetro arco de una hélice (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Distancia recorrida

2.2 Triedro intrínseco

2.3 Curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES