Una esfera conductora rellena de una densidad de carga

De Laplace

Contenido 1 Enunciado 2 Solución 2.1 Campo eléctrico 2.1.1 En el exterior de la esfera 2.1.2 En el interior de la esfera 2.2 Carga en la esfera conductora 2.3 Potencial en el centro de la esfera 2.3.1 A partir del campo eléctrico 2.3.2 Por integración directa 2.4 Energía electrostática almacenada

1 Enunciado

Una superficie esférica conductora de radio R, puesta a tierra, contiene en su interior una distribución de carga no uniforme, cuya densidad de carga es de la forma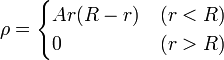

1. Calcule el campo eléctrico en todos los puntos del espacio.
2. Calcule el valor de la carga almacenada en la esfera conductora.
3. Halle el potencial eléctrico en el centro de la esfera.
   1. A partir del campo eléctrico.
   2. Por integración directa a partir de las densidades de carga.
4. Halle la energía electrostática almacenada en el sistema.

2 Solución

2.1 Campo eléctrico

Al haber una superficie conductora a tierra, que funciona como Jaula de Faraday, el problema se desacopla en dos independientes: el exterior de la esfera y el interior de ella.

2.1.1 En el exterior de la esfera

En el exterior del conductor se verifica la ecuación de Laplace, puesto que no hay carga exterior

    (r > R)

con las condiciones

        

La solución de la ecuación de Laplace en una región cuando el potencial se anula en todos los puntos de la frontera es simplemente

      

Dicho en términos físicos, la esfera conductora apantalla la densidad de carga interior, con el resultado de que en el exterior no se percibe campo alguno.

2.1.2 En el interior de la esfera

2.2 Carga en la esfera conductora

2.3 Potencial en el centro de la esfera

2.3.1 A partir del campo eléctrico

2.3.2 Por integración directa

2.4 Energía electrostática almacenada