Determinación de un vector a partir de sus proyecciones

De Laplace

1 Enunciado

Se tiene un vector conocido, no nulo, y uno que se desea determinar, 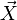. Se dan como datos su producto escalar y su producto vectorial por

Determine el valor de 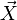. ¿Es suficiente una sola de las dos ecuaciones para hallar ?

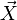2 Solución

Ante este problema existe la tentación de “pasar uno de los vectores al otro lado dividiendo”. Algo así

3 Interpretación geométrica