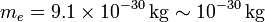Ejemplos de valores numéricos
De Laplace
Revisión a fecha de 18:03 25 sep 2011; Antonio (Discusión | contribuciones)
1 Enunciado
Las siguientes cantidades representan aproximadamente los valores de las magnitudes de la tabla, expresadas en las unidades fundamentales del SI o productos de ellas. Indique cuál le corresponde a cada una, indicando sus unidades.
| 1 | Peso de una persona | 2 | Densidad de masa del agua | 3 | Aceleración de la Tierra alrededor del Sol |
| 4 | Masa de la Tierra | 5 | Diámetro de un glóbulo rojo | 6 | Distancia Tierra-Sol |
| 7 | Altura a la que se encuentra la Estación Espacial Internacional | 8 | Radio de un átomo | 9 | Densidad del oro |
| 10 | Diámetro de una pelota de golf | 11 | Espesor de un folio | 12 | Aceleración de la gravedad |
| 13 | Volumen aproximado de oro en la Tierra | 14 | Velocidad de Usain Bolt en los 100m | 15 | Masa de un m³ de agua |
| 16 | Duración de un año | 17 | Velocidad de una bacteria | 18 | Periodo de la corriente alterna doméstica |
| 19 | Masa del electrón | 20 | Velocidad de la luz | 21 | Circunferencia terrestre |
| A | 10−30 | B | 10−10 | C | 6×10−6 |
| D | 5×10−5 | E | 6×10−3 | F | 2×10−2 |
| G | 5×10−2 | H | 10−1 | I | 10 |
| J | 10 | K | 8× 102 | L | 103 |
| M | 103 | N | 103 | O | 6×104 |
| P | 2×104 | Q | 5×105 | R | 3×107 |
| S | 4×107 | T | 3× 108 | U | 1.5×1011 |
2 Solución
Iremos colocando las parejas, sin un orden concreto, sino más bien por eliminación, comenzando por los valores más conocidos.
- 12-I. Aceleración de la gravedad
- El valor estándar de la aceleración de la gravedad es
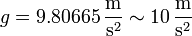
- 10-G. Diámetro de una pelota de golf
- De nuestra experiencia sabemos que ronda los 5 cm, estos es
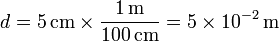
- 14-J. Velocidad de Usain Bolt en los 100m
- El récord mundial de los 100 metros lisos está en 9.58 s, lo cual da una velocidad media algo superior a 10 metros por segundo
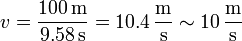
- 20-T. Velocidad de la luz
- La velocidad de la luz se suele dar como 300\ 000 km/s, que en las unidades fundamentales del SI equivale a

- 2-L. Densidad de masa del agua
- Es muy común oír “la densidad del agua es 1”, pero tal afirmación es incompleta pues no especifica las unidades. La densidad del agua es 1 g/cm³, que en las unidades fundamentales del Sistema Internacional queda
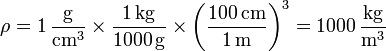
- 15-M. Masa de un m³ de agua
- A poco que uno lo piense, ve que esta pregunta es equivalente a la anterior
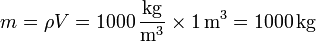
- 21-S. Circunferencia terrestre
- Una posibilidad consiste en usar el radio de la Tierra, cuyo valor medio es de 6370&thnsp;km:

- Otra posibilidad consiste en recordar que un metro se definió originalmente como “la diezmillonésima parte del cuadrante de meridiano terrestre”, esto es, que un cuarto de circunferencia terrestre tiene 10 millones de metros y por tanto
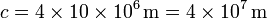
- 16-R. Duración de un año
- Esto es solo cuestión de multiplicar. Tenemos que un minuto dura 60 segundos. Una hora es
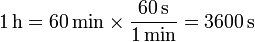
- Un día
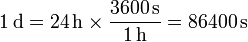
- y un año
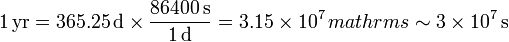
- Una regla sería decir que un siglo tiene π gigasegundos.
- 1-K. Peso de una persona
- Sobre esto lo primero sería decir que los pesos de las personas pueden ser muy variados, pero consideremos un peso medio de unos 70 kg. Vemos que en la tabla no hay ningún “70”. Observamos entonces que el enunciado habla de peso, no de masa. El pero de una persona de 70 kg sería

- Tampoco hay un 700 en la tabla, pero sí hay un 800, que sería el peso de una persona de 80 kg, por lo que decidimos que esta es la respuesta correcta.
- 6-U. Distancia Tierra-Sol
- Esta hay que sabérsela. Pero si uno no la sabe, basta con saber que es muy grande y ya hemos eliminado casi todos los números grandes. Queda el más grande de todos
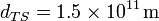
- o, como se expresa habitualmente, 150 millones de kilómetros. A esta distancia se la conoce como unidad astronómica (UA).
- 19-A. Masa del electrón
- De nuevo, viene bien conocerla de antemano. Pero si no, es suficiente saber que es minúscula, ya que la masa de un átomo, ya de por sí pequeña, está casi toda en sus protones y neutrones. La masa de un electrón es