Dinámica de la partícula (GIE)
De Laplace
Contenido |
1 Introducción
La Dinámica es la parte de la Mecánica que estudia el movimiento atendiendo a las causas que lo producen.
En principio, la Dinámica trata de cualquier sistema, formado por un número arbitrario de partículas, interactuando entre sí y con el fuerzas externas.
En este tema nos limitaremos a considerar la dinámica de una sola partícula (o punto material), considerada como cuerpo sin dimensiones y con una masa finita. A partir del estudio de la dinámica de partículas individuales puede tratarse el estudio de los sistemas de partículas y la dinámica del sólido rígido.
Dada la extensión del tema, lo estructuraremos en varios apartados:
- Leyes de Newton
- Análisis de problemas en dinámica
- Fuerzas de rozamiento
- Energía y leyes de conservación
- Aplicaciones de las leyes de Newton
- Estática de la partícula
- Equilibrio y estabilidad de la partícula (GIE)
2 Determinación de fuerzas
En ocasiones, conocemos completamente el estado de movimiento o de reposo de una partícula, bien porque hemos medido su posición y velocidad, bien porque se encuentra sometida a tres vínculos independientes que definen de forma unívoca el estado de la partícula.
En ese caso, la segunda ley de Newton nos sirve como herramienta para determinar la fuerza que actúa sobre la partícula.
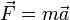
- Caso estático
- En el caso de una partícula en reposo (caso estático) la aceleración es nula, por lo que la resultante de las fuerzas aplicadas debe anularse. Si conocemos el valor de todas las fuerzas salvo una, podemos usar esta ecuación para hallar la fuerza desconocida.
- Este es el principio de los dinamómetros de resorte. Se aplica una fuerza que tensa un muelle. Se sabe que la fuerza que ejerce el resorte es proporcional a su elongación, por lo que debe cumplirse

- Midiendo cuánto se estira el muelle tenemos el valor de la fuerza.
- Caso dinámico
- Si tenemos una partícula en un movimiento conocido, podemos determinar la aceleración y a partir de ella determinar la fuerza que está actuando sobre la partícula.
- Por ejemplo, la tercera ley de Kepler establece que el cuadrado del periodo orbital de los planetas es proporcional al cubo de los radios de las órbitas.
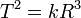
- Si suponemos órbitas circulares y que la fuerza es central (apunta permanentemente hacia el sol y sólo depende de la distancia al sol), entonces el movimiento es circular uniforme y
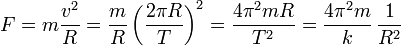
- Por tanto, la fuerza gravitatoria ejercida por el Sol debe ir como la inversa del cuadrado de la distancia, tal como afirma la ley de la Gravitación Universal.





