Estática de la partícula (GIE)

De Laplace

La estática es la parte de la mecánica que trata de las situaciones de equilibrio de los cuerpos. Un estado de equilibrio es aquél en el que el sistema se encuentra en reposo, permaneciendo en él indefinidamente.

El análisis del equilibrio de un sistema se compone de dos elementos:

• Establecer las condiciones en las que se produce el estado del equilibrio
• Establecer la estabilidad del equilibrio, esto es, determinar si el sistema, separado de su estado de equilibrio, vuelve a él o por el contrario se aleja de él.

1 Condición de equilibrio

Para el caso de una partícula material, la condición de equilibrio es una consecuencia inmediata de la segunda ley de Newton. Si la partícula se encuentra en un estado de reposo permanente, su aceleración es nula y por tanto

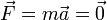
La condición de equilibrio de una partícula es que se anule la resultante de las fuerzas que actúan sobre ella.

Cuando tenemos fuerzas dependientes de la posición, este principio sirve para determinar las posiciones de equilibrio, mediante la solución de la ecuación

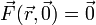
donde el segundo argumento de la fuerza es la velocidad, que será nula en una posición de equilibrio.

Por ejemplo, supongamos una masa sujeta a la acción de la gravedad y que cuelga de un resorte vertical, que verifica la ley de Hooke. Sumando las componentes verticales del peso y de la fuerza elástica tenemos que, en el equilibrio

      

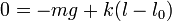
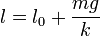
Si lo que se conoce es la posición de equilibrio y parte de las fuerzas actuantes, la condición de equilibrio sirve para determinar la fuerza restante.

2 Estabilidad del equilibrio

El que una posición sea de equilibrio no garantiza que, en una situación real, el sistema vaya a permanecer en ella indefinidamente. La razón es que siempre existen pequeñas fluctuaciones en las fuerzas, que pueden separar levemente al sistema del equilibrio. Para que el sistema permanezca en la misma posición, no basta con que su posición sea de equilibrio. Éste debe ser estable.

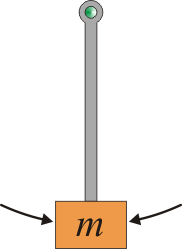
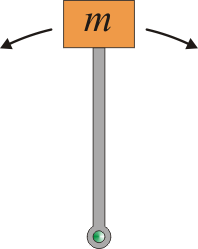
Consideremos, por ejemplo, un péndulo simple formado por una masa que cuelga de un punto de anclaje sujeto por una barra rígida sin masa. Este sistema posee dos posiciones de equilibrio: que la masa está en el punto más bajo del péndulo, o que esté en el punto más alto. Es claro que las dos posiciones no son equivalentes. Mientras que en la posición inferior la masa tiende a permanecer en ella, si se encuentra en el extremo superior cualquier pequeña perturbación hace que la masa caiga.

Estable	Inestable

Los puntos de equilibrio se clasifican en:

Estables

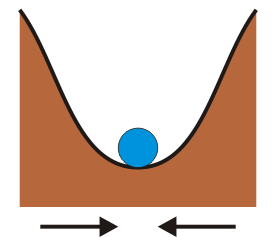
Ante una pequeña perturbación, tienden a retornar a la posición de equilibrio. El ejemplo representativo lo supone una partícula que rueda dentro de un cuenco, o una masa sujeta a un resorte.

Inestables

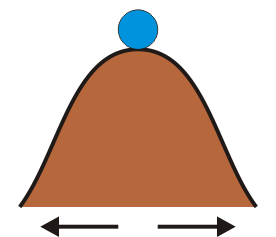
Una pequeña perturbación separa a la masa del equilibrio, y ésta tiende a alejarse de esta posición. Es el caso de una masa situada en lo alto de una cima o del péndulo invertido. También es el caso de una partícula en el interior de un tubo en rotación. Cuando se separa del centro, la inexistencia de una fuerza centrípeta hace que se aleje aun más.

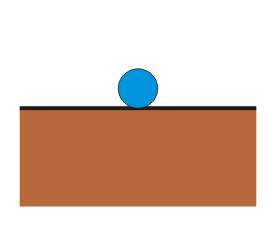
Indiferente

La partícula no tiende a retornar a la posición de equilibrio, pero tampoco a alejarse de ella. Es el caso de una bola situada sobre una mesa horizontal.

Estable	Inestable	Indiferente

La clasificación se complica en 3 dimensiones por el hecho de que una posición de equilibrio puede ser estable respecto a fuerzas aplicadas en una dirección e inestable frente a otras aplicadas en una diferente.

También puede ocurrir que una misma posición de equilibrio pueda ser estable para ciertos valores de los parámetros (por ejemplo, la masa de la partícula) e inestable para valores diferentes.

La forma más directa de abordar el problema de la estabilidad consiste en suponer una posición muy próxima a la de equilibrio y analizar el sentido de la fuerza para un desplazamiento dado. Por ejemplo, en el caso del resorte que cuelga verticalmente hacemos

      

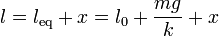
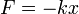
Esto quiere decir que cuando x es positivo, la fuerza es negativa, es decir, tiende a disminuir |x|. Igualmente, si x es negativo, F es positiva, con lo que también tiende a disminuir |x|. El punto de equilibrio es, por tanto, estable.

Una de las herramientas más intuitivas para el análisis de la estabilidad es el uso de las curvas de energía potencial, que veremos al analizar la ley de conservación de la energía mecánica.