Dos placas conductoras y una densidad de carga intermedia
De Laplace
Contenido |
1 Enunciado
Dos placas metálicas, planas y paralelas, de sección S, se encuentran situadas a una distancia $a$ la una de la otra. La placa inferior se pone a una tensión V1, mientras que la superior se encuentra a tensión V2. El espacio entre las placas está ocupado por una capa de un material cargado con una densidad uniforme ρ0.
- Determine el potencial y el campo eléctrico en todos los puntos entre las placas.
- Calcule la energía eléctrica almacenada en el sistema.
- Halle la fuerza sobre las placas y sobre el material intermedio.
2 Solución
2.1 Potencial y campo eléctrico
2.1.1 Potencial
En este problema debemos resolver la ecuación de Poisson
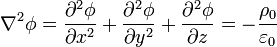
con condiciones de contorno de Dirichlet

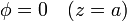
Dado que ni la densidad de carga ni las condiciones de contorno dependen de x ni de y, salvo en el hecho de que las placas tienen una extensión S, podemos hacer la aproximación de despreciar los efectos de borde y suponer que el potencial depende exclusivamente de la coordenada z. Esto reduce la ecuación de Poisson a

con solución
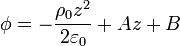
Las constantes A y B las obtenemos de las condiciones de contorno
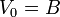

resultando finalmente las constantes y el potencial
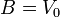
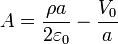
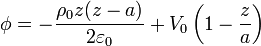
Esta solución puede escribirse como la superposición
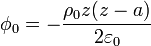
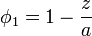
siendo 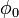 el potencial que habría entre las placas si estuviera presente la carga pero los conductores estuvieran a tierra.
el potencial que habría entre las placas si estuviera presente la carga pero los conductores estuvieran a tierra. 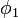 representa el potencial que habría si la carga estuviera ausente, la placa inferior estuviera a potencial unidad y la superior a tierra.
representa el potencial que habría si la carga estuviera ausente, la placa inferior estuviera a potencial unidad y la superior a tierra.
2.1.2 Campo
Conocido el potencial determinamos el campo a partir de su gradiente
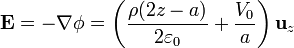
Este campo varía linealmente desde un valor

en z = 0 hasta
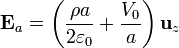
en z = a.





