Cubo entre cuatro placas conductoras
De Laplace
Contenido |
1 Enunciado
Cuatro placas cuadradas de lado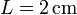 
, conductoras, se encuentran en la disposición cuadrada indicada en la figura.
Entre las cuatro placas, centrado, se encuentra un cubo conductor, de arista 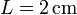, situado a una distancia 
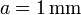de cada placa. El cubo está descargado en todo momento.
Si las cuatro placas se conectan a sendos generadores que fijan tensiones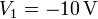 
, 
, 
, 
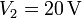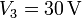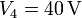
- Halle la carga almacenada en cada una de las placas cuadradas.
- Calcule la energía electrostática del sistema.
- Calcule el valor del campo en cada uno de los condensadores que se forman.
- Halle la presión electrostática en cada cara del cubo enfrentada a una placa, así como la fuerza electrostática total sobre el cubo.
Despréciense los efectos de borde y los debidos a las caras del cubo no enfrentadas a una placa.
2 Solución
2.1 Carga almacenada en las placas
La forma más sencilla de abordar este problema es con ayuda de un circuito equivalente.
Tenemos cinco conductores, equivalentes a cinco nodos del circuito: las cuatro placas (que etiquetaremos de “1” a “4”) y el cubo central (que será el conductor “5”).
En principio, el circuito equivalente se compone de 10 condensadores, uno entre cada dos nodos, más 5 con el infinito.
Sin embargo, se nos dice que despreciemos los efectos de borde. Esto equivale a admitir que sólo hay campo eléctrico en los espacios entre las placas planas y el cubo. Por tanto, el sistema se reduce a solo cuatro condensadores: los que forman cada placa con el cubo. La capacidad de todos estos condensadores es la misma:
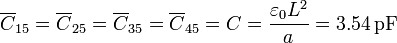
La presencia del cubo apantalla unas placas respecto de las otras
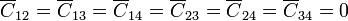
y la aproximación de que se desprecien los efectos de borde hace que no haya que considerar los condensadores que cada placa forma con el infinito.
Además, como se nos dice en el enunciado la misma aproximación nos permite despreciar el efecto de las caras del cubo no enfrentadas a placas, por lo que
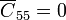
Por tanto el circuito equivalente tiene cinco nodos y cuatro condensadores. A esto hay que añadirle las cuatro fuentes de tensión conectadas a sendas placas.
El cubo central posee carga constante Q = 0 por lo que habría que conectar a su nodo una fuente de carga. Sin embargo, al tratarse de carga nula podemos prescindir de ella.
A partir de este circuito podemos obtener la carga en cada placa como
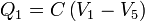
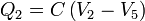
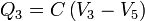
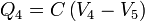
Eliminando paréntesis obtenemos la matriz de coeficientes de capacidad
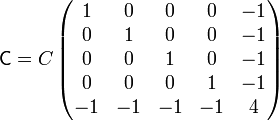
Vemos que, como debe ser, los términos de la diagonal principal son estrictamente positivos, mientras que los no diagonales son negativos nulos.
De la condición de que el cubo está descargado obtenemos el valor de su potencial
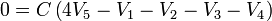
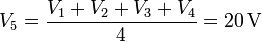
Una vez que tenemos el potencial del cubo, que resulta ser la media aritmética de los de las cuatro placas, el cálculo de la carga de cada placa es inmediato
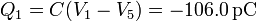
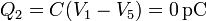
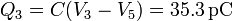
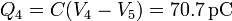
Obsérvese que la suma de las cuatro cargas es 0, ya que hay tanta carga en las placas como en el cubo, cambiada de signo. Puesto que el cubo está descargado, la suma de las cargas de las placas es también nula.
2.2 Energía electrostática
Conocidas la carga y el potencial de cada conductor, el cálculo de la energía es inmediato:
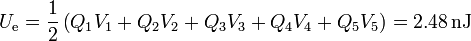
Esta misma cantidad puede calcularse a partir de la energía almacenada en un conjunto de condensadores
