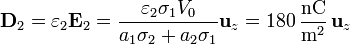Resistor con dos capas

De Laplace

Revisión a fecha de 19:32 10 jun 2011; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Densidades de corriente y campos
3 Intensidad de corriente
4 Carga libre
5 Potencia y energía
6 Solución mediante el circuito equivalente

1 Enunciado

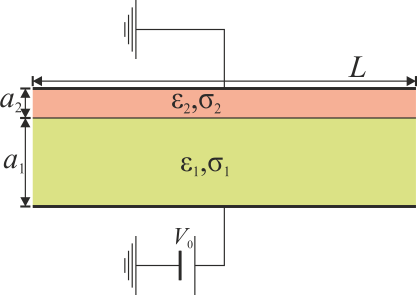
Se tiene un dispositivo formado por dos placas metálicas perfectamente conductoras, de sección cuadrada de lado 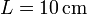$L=10\,\mathrm{cm}$ situadas paralelamente a 4\,mm de distancia

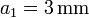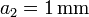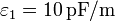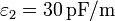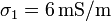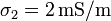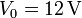Entre las placas se encuentran dos capas de dieléctricos no ideales de espesor $a_1=3\,\mathrm{mm}$ y $a_2=1\,\mathrm{mm}$ , respectivamente, de permitividades $\varepsilon_1 = 10\,\mathrm{pF}/\mathrm{m}$ y $\varepsilon_2=30\,\mathrm{pF}/\mathrm{m}$ y conductividades $\sigma_1=6\,\mathrm{mS}/\mathrm{m}$ y $\sigma_2=2\,\mathrm{mS}/\mathrm{m}$ . Se aplica un voltaje constante entre las placas $V_0 = 12\,\mathrm{V}$ .

Determine el valor de la densidad de corriente, el campo eléctrico y el vector desplazamiento en todos los puntos entre las placas.
Halle la intensidad de corriente que atraviesa el dispositivo.
Calcule las densidades de carga libre en todos los medios y superficies del sistema, así como la carga libre total acumulada en cada uno de los medios y superficies.
Halle la potencia disipada y la energía almacenada en el sistema.

2 Densidades de corriente y campos

Este sistema es uno de corrientes estacionarias, al estar las placas sometidas a una diferencia de potencial constante. Por ello, lo que va a determinar la distribución de los campos son las conductividades de los medios. El sistema equivale a dos resistencias puestas en serie para el cálculo de la densidad de corriente y el campo eléctrico.

En principio tenemos, para cada medio, las ecuaciones

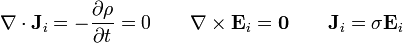
$\nabla\cdot\mathbf{J}_i = -\frac{\partial\rho}{\partial t} = 0\qquad\nabla\times\mathbf{E}_i = \mathbf{0}\qquad \mathbf{J}_i=\sigma\mathbf{E}_i$

Dado que la anchura de las placas es mucho mayor que la distancia entre ellas y que la interfaz es también paralela a las placas podemos suponer que los campos van en la dirección perpendicular a las placas, que tomaremos como eje Z

$\mathbf{E}_i = E_i\mathbf{u}_z\qquad\mathbf{J}_i = J_i\mathbf{u}_z$

Al sustituir esto en las ecuaciones diferenciales anteriores el resultado es, como en otros problemas, que las distribuciones de campo son uniformes en cada uno de los medios (aunque pueden tener un valor diferente en cada uno de ellos).

Queda hallar el valor de las constantes $E 1$ y $E 2$ . Para ello tenemos, en primer lugar, que la diferencia de potencial entre placas es $V 0$

$V_0 = \int_0^{a_1+a_2}E\,\mathrm{d}z = \int_0^{a_1}E\,\mathrm{d}z + \int_{a_2}^{a_1+a_2}E\,\mathrm{d}z = E_1a_1+E_2a_2$

En segundo lugar tenemos que en el estado estacionario no cambia la carga acumulada en la interfaz aentre los medios

$\mathbf{n}\cdot[\mathbf{J}] = -\frac{\partial\sigma_s}{\partial t} = 0\qquad\Rightarrow\qquad J_1 = J_2=J_0$

esto es, la densidad de corriente es la misma en las dos regiones. Hallamos el valor de J_0 sustituyendo en la ecuación anterior

$E_1 = \frac{J_0}{\sigma_1}\qquad E_2 = \frac{J_0}{\sigma_2}\qquad a_1\frac{J_0}{\sigma_1}+a_2\frac{J_0}{\sigma_2}=V_0$

Despejando

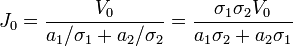
$J_0=\frac{V_0}{a_1/\sigma_1+a_2/\sigma_2}= \frac{\sigma_1\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}$

Por tanto, la densidad de corriente en los dos medios es, sustituyendo los valores numéricos,

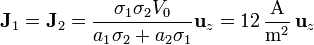
$\mathbf{J}_1 = \mathbf{J}_2 = \frac{\sigma_1\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z = 12\,\frac{\mathrm{A}}{\mathrm{m}^2}\,\mathbf{u}_z$

El campo eléctrico en la capa inferior vale

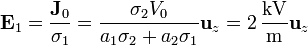
$\mathbf{E}_1 = \frac{\mathbf{J}_0}{\sigma_1} = \frac{\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z = 2\,\frac{\mathrm{kV}}{\mathrm{m}}\mathbf{u}_z$

y en la superior

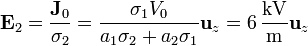
$\mathbf{E}_2 = \frac{\mathbf{J}_0}{\sigma_2} = \frac{\sigma_1V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z = 6\,\frac{\mathrm{kV}}{\mathrm{m}}\mathbf{u}_z$

De aquí obtenemos que la diferencia de potencial entre la interfaz y la placa de tierra es

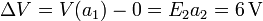
$\Delta V = V(a_1) - 0 = E_2a_2 = 6\,\mathrm{V}$

Una vez que tenemos el campo eléctrico, el vector desplazamiento es inmediato. En el medio inferior

$\mathbf{D}_1 = \varepsilon_1\mathbf{E}_1 = \frac{\varepsilon_1\sigma_2V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z= 20\,\frac{\mathrm{nC}}{\mathrm{m}^2}\,\mathbf{u}_z$

y en el superior

$\mathbf{D}_2 = \varepsilon_2\mathbf{E}_2 = \frac{\varepsilon_2\sigma_1V_0}{a_1\sigma_2+a_2\sigma_1}\mathbf{u}_z= 180\,\frac{\mathrm{nC}}{\mathrm{m}^2}\,\mathbf{u}_z$

3 Intensidad de corriente

4 Carga libre

5 Potencia y energía

6 Solución mediante el circuito equivalente

Resistor con dos capas

De Laplace

Contenido

1 Enunciado

2 Densidades de corriente y campos

3 Intensidad de corriente

4 Carga libre

5 Potencia y energía

6 Solución mediante el circuito equivalente

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES