Entrar Página Discusión Historial Go to the site toolbox

Cálculo de las fuentes de un campo magnético

De Laplace

Contenido

1 Enunciado

En el espacio alrededor de una esfera superconductora existe un campo magnético de la forma

\mathbf{B}(\mathbf{r})=\begin{cases} \mathbf{0} & (r < a) \\ & \\ B_0\left(\left(1+\displaystyle\frac{C_1}{r^3}\right)\cos(\theta)\mathbf{u}_r+ \left(-1+\displaystyle\frac{C_2}{r^3}\right)\mathrm{sen}(\theta)\mathbf{u}_\theta\right) & (r>a) \end{cases}
  1. Calcule los valores de las constantes C1 y C2.
  2. Determine las corrientes que crean este campo.
  3. ¿A qué tiende este campo para r \gg a?
  4. Este campo puede escribirse como el del apartado anterior, más el campo de un dipolo magnético. ¿Cuánto vale su momento dipolar magnético?

2 Valores de las constantes

Los valores de C1 y C2 los calculamos imponiendo que éste sea un campo magnético. Las ecuaciones que debe verificar necesariamente son:

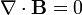
\nabla\cdot\mathbf{B}=0        \mathbf{n}\cdot[\mathbf{B}] = 0

La primera debe cumplirse en todo volumen y la segunda en toda superficie de discontinuidad, que en este caso es solamente la superficie esférica r = a.

2.1 Ecuación volumétrica

La ley de Gauss para el campo magnético se cumple idénticamente en la esfera r < a, por ser nulo el campo en ella.

\nabla\cdot\mathbf{B} = \nabla\cdot\mathbf{0} = 0\qquad (r < a)

En el exterior de la esfera en cambio, debemos recurrir a la expresión de la divergencia, calculada en coordenadas esféricas

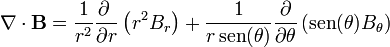
\nabla\cdot\mathbf{B} = \frac{1}{r^2}\frac{\partial\ }{\partial r}\left(r^2B_r\right) + \frac{1}{r\,\mathrm{sen}(\theta)}\frac{\partial }{\partial\theta}\left(\mathrm{sen}(\theta)B_\theta\right)

Hallamos cada término por separado. Para el primero

\frac{1}{r^2}\frac{\partial\ }{\partial r}\left(r^2B_r\right) = \frac{1}{r^2}\frac{\partial\ }{\partial r}\left(B_0\left(r^2+\displaystyle\frac{C_1}{r}\right)\cos(\theta)\right) = B_0\left(\frac{2}{r}-\frac{C_1}{r^4}\right)\cos(\theta)

y para el segundo

\frac{1}{r\,\mathrm{sen}(\theta)}\frac{\partial }{\partial\theta}\left(\mathrm{sen}(\theta)B_\theta\right) = \frac{1}{r\,\mathrm{sen}(\theta)}\frac{\partial }{\partial\theta}\left(B_0\left(-1+\displaystyle\frac{C_2}{r^3}\right)\mathrm{sen}^2(\theta)\right) = B_0\left(-\frac{2}{r}+\frac{2C_2}{r^4}\right)\cos(\theta)

La suma de estos dos términos da

\nabla\cdot\mathbf{B} = \frac{B_0(-C_1+2C_2)}{r^4}\cos(\theta)\qquad (r>a)

Para que esta divergencia se anule, debe ser

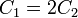
C_1 = 2C_2\,

2.2 Condición de salto

La otra ecuación la da la condición de que la componente normal del campo sea continua en cualquier superficie. Puesto que el campo en el interior de la esfera es nulo, esto implica que la componente normal justo en el exterior de la superficie esférica también debe anularse, esto es, el campo debe ser puramente tangencial a la superficie.

Imponemos la condición de salto

0 = \mathbf{n}\cdot[\mathbf{B}] = \mathbf{u}_r\cdot\left(B_0\left(\left(1+\displaystyle\frac{C_1}{a^3}\right)\cos(\theta)\mathbf{u}_r + \left(-1+\displaystyle\frac{C_2}{a^3}\right)\mathrm{sen}(\theta)\mathbf{u}_\theta\right)-\mathbf{0}\right)

Obsérvese que hay que sustituir el valor de la coordenada r por su valor, a, en la superficie esférica. La coordenada θ, en cambio, se deja tal cual, pues en la superficie esférica, la coordenada polar tiene todos los valores posibles, no uno solo. Al hacer el producto escalar, la componente polar del campo no contribuye y queda simplemente la condición

0 = B_0\left(1+\displaystyle\frac{C_1}{a^3}\right)\cos(\theta)

de donde

C_1 = -a^3\qquad C_2 = -\frac{a^3}{2}

2.3 Expresión del campo

Sustituyendo los valores de las constantes obtenemos la expresión del campo en todos los puntos del espacio

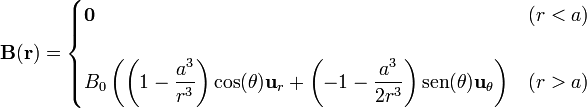
\mathbf{B}(\mathbf{r})=\begin{cases} \mathbf{0} & (r < a) \\ & \\ B_0\left(\left(1-\displaystyle\frac{a^3}{r^3}\right)\cos(\theta)\mathbf{u}_r+ \left(-1-\displaystyle\frac{a^3}{2r^3}\right)\mathrm{sen}(\theta)\mathbf{u}_\theta\right) & (r>a) \end{cases}

Justo en la superficie exterior de la esfera este campo se reduce a

\mathbf{B}(a^+) = -\frac{3B_0}{2}\mathrm{sen}(\theta)\mathbf{u}_\theta

3 Fuentes del campo

Una vez que tenemos el campo, podemos calcular las fuentes que lo producen. Estas son necesariamente vectoriales y pueden ser volumétricas o de superficie. Su expresión viene dada por la ley de Ampère

\mathbf{J} = \frac{1}{\mu_0}\nabla\times\mathbf{B}\qquad \qquad\mathbf{K}=\frac{1}{\mu_0}\mathbf{n}\times[\mathbf{K}]

3.1 Densidad volumétrica

La densidad de corriente de volumen es nula en el interior de la esfera, por ser el campo nulo

\mathbf{J} = \frac{1}{\mu_0}\nabla\times\mathbf{B} = \frac{1}{\mu_0}\nabla\times\mathbf{0}=\mathbf{0}\qquad (r<a)

En el exterior, empleamos la expresión del rotacional en coordenadas esféricas:

\mathbf{J} = \frac{1}{\mu_0}\nabla\times\mathbf{B} = \frac{1}{\mu_0r^2\mathrm{sen}(\theta)}\left|\begin{matrix}0 & 0 & 0\\ & & \\ 0 & 0 & 0 \\ & & \\ B_r & rB_\theta & 0\end{matrix}\right|
No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \mathbf{J} = \frac{1}{\mu_0}\nabla\times\mathbf{B} = \frac{1}{\mu_0r^2\mathrm{sen}(\theta)}\left|\begin{matrix}\mathbf{u}_r & r\mathbf{u}_\theta & r\,\mathrm{sen}(\theta)\mathbf{u}_\varphi} \\ & & \\ \displaystyle\frac{\partial }{\partial r} & \displaystyle\frac{\partial }{\partial \theta} & 0 \\ && \\ B_r & rB_\theta & 0\end{matrix}\right|

4 Comportamiento asintótico del campo

5 Momento dipolar magnético

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_las_fuentes_de_un_campo_magn%C3%A9tico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace