Cálculo de las fuentes de un campo magnético
De Laplace
Revisión a fecha de 18:14 14 may 2011; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
En el espacio alrededor de una esfera superconductora existe un campo magnético de la forma

- Calcule los valores de las constantes C1 y C2.
- Determine las corrientes que crean este campo.
- ¿A qué tiende este campo para
 ?
?
- Este campo puede escribirse como el del apartado anterior, más el campo de un dipolo magnético. ¿Cuánto vale su momento dipolar magnético?
2 Valores de las constantes
Los valores de C1 y C2 los calculamos imponiendo que éste sea un campo magnético. Las ecuaciones que debe verificar necesariamente son:
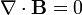
![\mathbf{n}\cdot[\mathbf{B}] = 0](/wiki/images/math/c/8/2/c82827f0b3e04bed75d70b5a389b9608.png)
La primera debe cumplirse en todo volumen y la segunda en toda superficie de discontinuidad, que en este caso es solamente la superficie esférica r = a.
2.1 Ecuación volumétrica
La ley de Gauss para el campo magnético se cumple idénticamente en la esfera r < a, por ser nulo el campo en ella.

En el exterior de la esfera en cambio, debemos recurrir a la expresión de la divergencia, calculada en coordenadas esféricas