Ecuaciones de Maxwell FII GIA
De Laplace
Contenido |
1 Introducción
Los fenómenos electromagnéticos que hemos visto hasta ahora se pueden explicar con cuatro leyes básicas. Estas leyes, en su expresión integral, son
1.1 Ley de Gauss
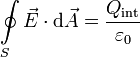
En esta ley se resumen varios datos sobre el campo eléctrico
- Las cargas eléctricas crean campo eléctrico.
- Las líneas de campo eléctrico mueren en las cargas positivas y mueren en las cargas negativas.
- El campo eléctrico se calcula a partir de la distribución de carga eléctrica.
1.2 Ley de Gauss magnética
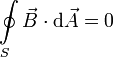
En esta ley se resumen varios datos sobre el campo magnético
- No existen cargas magnéticas.
- Las líneas de campo magnético son líneas cerradas.
1.3 Ley de Faraday
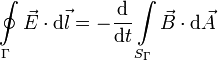
La letra Γ representa una línea cerrada, y SΓ es una superficie apoyada en esa línea.
En esta ley se expresa el hecho de que un campo magnético variable en el tiempo es capaz de producir un campo eléctrico. Por tanto, hay dos fuentes de campo eléctrico: las cargas eléctricas y un campo magnético variable en el tiempo.
1.4 Ley de Ampère
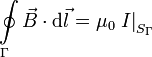
Aquí, Γ representa una línea cerrada y 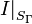 es la corriente eléctrica que atraviesa una superficie cualquiera apoyada en la línea Γ.
es la corriente eléctrica que atraviesa una superficie cualquiera apoyada en la línea Γ.
Esta ley nos dice que
- Las corrientes eléctricas generan campos magnéticos.
- Las líneas de campo magnético generado por estas corrientes dan vueltas alrededor de las corrientes.
- El campo magnético se puede calcular a partir de la distribución de corriente eléctrica.
2 Corriente de desplazamiento
De las cuatro leyes que hemos visto en el apartado anterior, hay una de ellas que no es completamente correcta. Se trata de la ley de Ampère
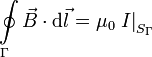
Esta ley dice que la circulación del campo magnético a lo largo de una curva cerrada Γ es igual a la corriente eléctrica que atraviesa una superficie SΓ que se apoye en esa curva. Sin embargo, para una curva cerrada cualquiera hay un número infinito de superficies que se apoyan en ella.
2.1 Hilo inifinito
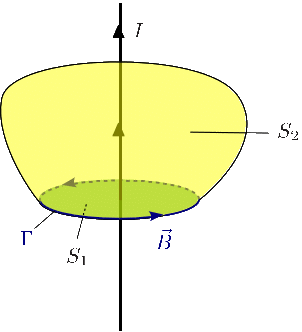
Consideremos la situación de un hilo infinito por el que circula una corriente I. Escogemos como curva cerrada una circunferencia centrada en el hilo, que en cada punto es paralela al campo magnético. Las dos superficies de la figura se apoyan en la curva. La superfice S1 es el círculo definido por la circunferencia y la superfice S2 es una especia de boina amarilla.
Las dos superficies son atravesadas por la misma corriente, de modo que si consideramos la superficie S1 tenemos
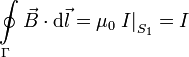
Mientras que si consideramos la superficie S2 tenemos
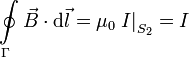
Es decir, en este caso la Ley de Ampère se cumple cualquiera que sea la superficie escogida.
2.2 Hilo y condensador
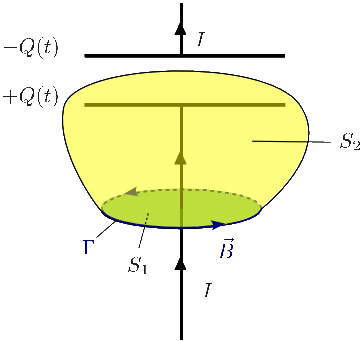
Consideremos ahora la situación de la figura. El hilo está conectado a un condensador, de modo que la corriente I está depositando carga en las placas del condensador. Consideramos una situación en que la corriente depende del tiempo, pues en situación estacionaria el condensador actúa como un abierto y no puede haber corriente en el cable.
Observamos que en este caso la corriente no atraviesa la superficie S2, pues las cargas no se pueden mover en el interior del condensador. Si ahora aplicamos la Ley de Ampére en la superficie S1 tenemos
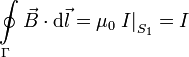
Mientras que si lo hacemos en la superficie S2 tenemos
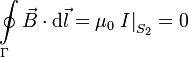
¿Como arreglamos esta discrepancia?
La ley de Ampère dice que las corrientes eléctricas crean campos magnéticos. El problema podría arreglarse si añadimos otro término al lado derecho de la Ley de Ampère, es decir, si encontramos otra fuente de campo magnético.
La pista la da la Ley de Faraday. Esta dice que un flujo magnético variable en el tiempo crea en el que campo eléctrico. Razonando por analogía, podemos postular que un flujo de campo eléctrico puede crear un campo magnético. De este modo, definimos la corriente de desplazamiento como
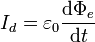
donde
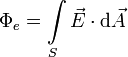
es el flujo del campo elétrico que atraviesa la superfice S. La ley de Ampére modificada queda así
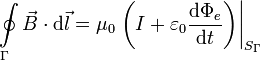
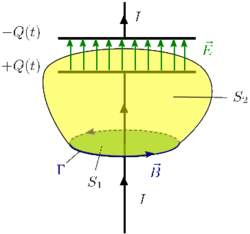
Ahora al aplicar la Ley de Ampère con la superfice S1 la corriente eléctrica que la atraviesa es I y el flujo eléctrico es nulo. Al aplicarla con la superficie S2 la corriente eléctrica que la atraviesa es nula mientras que la derivada del flujo eléctrico no lo es
En la superficie S1 tenemos
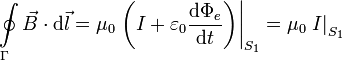
Mientras que si lo hacemos en la superficie S2 tenemos
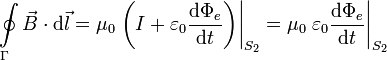
En el problema 2 del boletín vemos que los dos términos derechos son iguales.
La nueva versión de la ley se llama Ley de Ampère-Maxwell, en honor de James C. Maxwell, que enunció las ecuaciones que llevan su nombre.
Puede parecer que hemos demostrado la existencia de la corriente de desplazamiento, pero no es así. Hemos postulado que existe la corriente de desplazamiento. Sabemos que esta corriente existe porque la ley obtenida la introducirla (la Ley de Ampère-Maxwell) describe correctamente los hechos experimentales.
3 Ecuaciones de Maxwell
Podemos enunciar ahora las cuatro ecuaciones de Maxwell en su formulación integral
Ley de Gauss
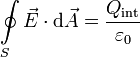
Ley de Gauss magnética
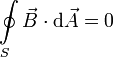
Ley de Faraday
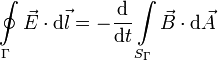
Ley de Ampère-Maxwell
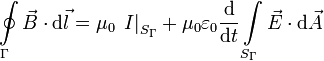
Los términos de la derecha de estas ecuaciones describen las fuentes que producen los campos que aparecen en los términos de la izquierda. Así, un campo eléctrico puede ser creado por cargas eléctricas (Ley de Gauss) o por un campo magnético variable en el tiempo (Ley de Faraday). Y un campo magnético puede ser creado por una corriente o por un campo eléctrico variable en el tiempo (Ley de Ampére-Maxwell).
Para completar la descripción teórica del Electromagnetismo hay que incluir la Ley de Lorentz, que describe la fuerza que los campo ejercen sobre las cargas eléctricas. Así, la fuerza que una carga puntual q con velocidad  sufre cuando se mueve bajo la acción de un campo eléctrico y campo magnético es
sufre cuando se mueve bajo la acción de un campo eléctrico y campo magnético es
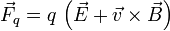
4 Ondas electromagnéticas en el vacío
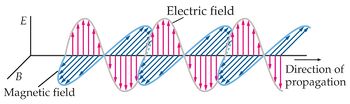
La ley de Faraday dice que un campo magnético variable en el tiempo produce un campo eléctrico, en general también variable en el tiempo. La adición de la corriente de desplazamiento en la Ley de Ampère-Maxwell implica que un campo eléctrico variable en el tiempo produce un campo magnético, en general también variable en el tiempo. Esta producción cruzada de campos eléctricos y magnéticos es lo que permite la existencia de ondas electromagnéticas.
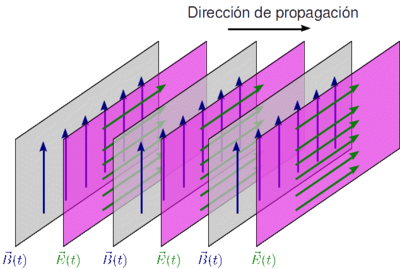
La figura da una explicación cualitativa de las ondas electromagnéticas. Si tenemos un campo magnético variable en el tiempo (primer plano empezando por la izquierda), por la Ley de Faraday produce un campo eléctrico variable en el tiempo (segundo plano por la izquierda). A su vez, por la ley de Ampère-Maxwell, este campo eléctrico produce un campo magnético (tercer plano por la izquierda) que a su vez produce un campo eléctrico (cuarto plano por la izquierda) y así sucesivamente. El resultado es una serie de campos eléctricos y magnéticos que se "apoyan" unos sobre otros y se propagan en la dirección indicada en la figura. El vector que indica la dirección y sentido de propagación de la onda es paralelo al producto vectorial del campo eléctrico y el magnético
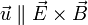
Este es un ejemplo de onda plana, en el que los campos se disponen en planos perpendiculares a la dirección de propagación. Los campos eléctricos y magnéticos son perpendiculares entre sí y a la dirección de propagación. Es decir, es una onda transversal. A partir de las Ecuaciones de Maxwell puede demostrarse que los campo eléctricos y magnéticos cumplen la siguiente ecuación diferencial
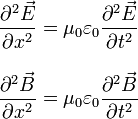
Hemos escogido el eje X coincidente con la dirección de propagación.
Estas son ecuaciones de onda, como vimos en el tema de Ondas. Comparando con la ecuación de ondas genérica
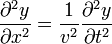
vemos que la velocidad de las ondas electromagnéticas en el vacío es
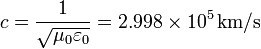
Cuando Maxwell encontró estas ecuaciones, se dio cuenta de que había descubierto un nuevo tipo de ondas. Al calcular numéricamente esta velocidad, descubrió que su valor era muy próximo a la velocidad de la luz que se había medido experimentalmente poco antes. Entonces llegó a la conclusión de la que la luz es una onda electromagnética, realizando de este modo la unificación entre la Óptica y el Electromagnetismo.
Esta velocidad es para ondas en el vacío, es decir, sin que haya medios materiales. Cuando la luz se propaga en un medio material (aire, agua, vidrio, etc) la velocidad disminuye. Si el medio es lineal, la velocidad es
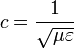
Aquí, μ es la permeabilidad magnética del medio, y  es su permitividad eléctrica.
es su permitividad eléctrica.
Los módulos del campo eléctrico y el campo magnético en una onda están relacionados por la expresión
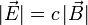
Debido al gran valor de c, el valor numérico del módulo del campo magnético es mucho más pequeño que el del campo magnético.
4.1 Espectro electromagnético
Las soluciones de la ecuación de onda electromagnética puede escribirse siempre como superposición de ondas armónicas. Para el campo eléctrico tendríamos
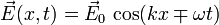
El signo menos representa una onda que viaja en sentido positivo del eje X mientras que el signo positivo corresponde a una onda viajando en el sentido negativo del eje. El número de ondak y la frecuencia angular ω están relacionados con la longitud de onda y el período
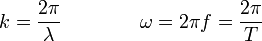
La longitud de onda λ y la frecuencia natural f están relacionadas por la velocidad de propagación
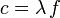
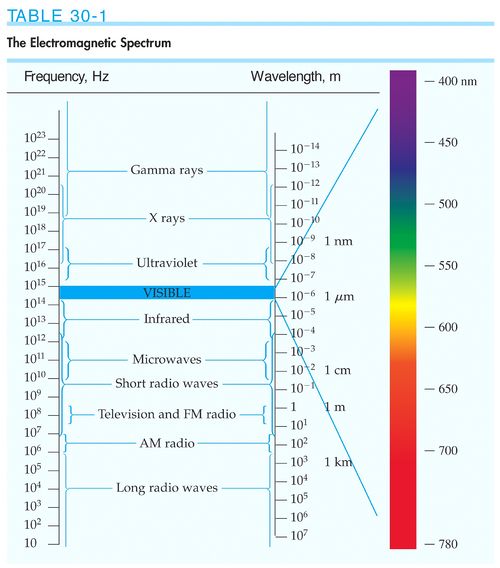
Los rayos X, los rayos γ, la luz visible, la radiación infrarroja y ultravioleta, las ondas de radio, televisión y telefonía movil...son ondas electromagnéticas. La diferencia entre ellas es la frecuencia y la longitud de onda. El espectro electromagnético se divide en zonas según el tipo de ondas que se considere. Estás zonas no están claramente separadas. Por ejemplo los rayos γ y los rayos X se solapan en el espectro.
La interacción entre las ondas electromagnéticas y la materia depende de la frecuencia de la onda. Nuestros fotoreceptores oculares están adaptados para detectar las longitudes en el rango entre 400 y 780 nm, por lo que esta región del espectro recibe el nombre de espectro visible. Los cuerpos calientes emiten ondas en el infrarrojo. La frecuencia de los rayos X y γ corresponde a niveles energéticos de los enlaces moleculares del ADN. Por eso es peligroso exponerse a estos rayos, pues pueden producir mutaciones en el ADN. El vidrio es transparente en el espectro visible, pero no así en el ultravioleta, donde absorbe gran parte de las ondas que lo atraviesan.
La frecuencia de la onda está determinada por el proceso físico que la genera. Los rayos γ provienen de interacciones subatómicas, aniquiliaciones de materia y antimateria o reacciones nucleares de fusión y fsisión, entre otras fuentes. Los rayos X son producidos por cargas eléctricas sometidas a una gran aceleración, como ocurre en los tubos de rayos X o en galaxias con grandes campos magnéticos. Los cuerpos calientes emiten ondas en el espectro infrarrojo, mientras que las antenas de telefonía móvil y los hornos de microondas emiten ondas con longitudes de onda del orden del centímetro.