Esfera polarizada uniformemente
De Laplace
Contenido |
1 Enunciado
Se tiene una esfera dieléctrica de radio R polarizada uniformemente con 
.
- Halle, por integración directa el potencial eléctrico en todos los puntos del espacio.
- ¿Cuáles son los valores de
, 
y 
dentro y fuera de la esfera?
- ¿Cuánto valen las densidades de carga equivalentes a la polarización?
2 Solución
2.1 Potencial eléctrico
Para hallar el potencial por integración directa debemos emplear el hecho de que el potencial creado por un dipolo puntual es
donde 
es el vector que va desde el punto donde se encuentra el dipolo al punto en que se mide el potencial.
Si tenemos una distribución de dipolos, descrita por la polarización \mathbf{P} el potencial total será la integral
No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int\frac{{\bf P}(\mathbf{r}'){\cdot}(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\mathrm{d}\tau'
donde la integral se calcula sobre todos los puntos donde la polarización no es nula. Esta expresión es análoga a la que se da para una distribución de carga a partir del potencial de una carga puntual.
En nuestro caso dentro de la esfera y cero fuera, por lo que podemos sacar la polarización fuera de la integral y escribir el potencial como
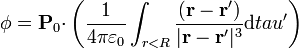
donde la integral se calcula en la esfera de centro el origen y radio R.
La integral que debemos calcular es bastante complicada. Así, por ejemplo, la componente z podemos expresarla en esféricas y escribirla como
con
No obstante, podemos ahorrarnos todo el cálculo si en este punto recordamos que el campo creado por una cierta distribución de carga es
y, en particular si tenemos una distribución de carga uniforme unitaria en una esfera de radio R (ρ = 1 dentro y cero fuera) el campo es
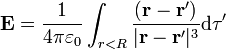
Ésta es precisamente la integral que aparece multiplicando a 
en la expresión del potencial. Por tanto, a partir del conocimiento de dicho campo podemos calcular el potencial en nuestro problema. Pero el valor del campo creado por una esfera de carga es conocido.
Su valor es
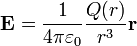
con Q(r) la carga encerrada dentro de una esfera de radio r. En nuestro caso esto da
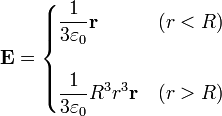
por lo que el potencial de nuestro problema es
\phi=\begin{cases}\displaystyle\frac{\mathbf{P}_0\cdot\mathbf{r}}{3\varepsilon_0} & (r<R)\\ & \\ \displaystyle\frac{R^3\mathbf{P}_0\cdot\mathbf{r}}{3\varepsilon_0r^3} & (r>R)\end{cases} \] y ya está resuelto el problema.
{{subst:nota}} Obsérvese que en ningún momento se dice que el campo debido a una distribución de dipolos sea el de una esfera de carga uniforme. Lo único que se hace es emplear este último campo como herramienta de cálculo para hallar el potencial de la distribución de dipolos. </div>
