Dos conductores enfrentados

De Laplace

1 Enunciado

Se colocan enfrentados dos conductores metálicos de forma arbitraria. No hay más conductores ni cargas en el sistema. Halle el signo de las dos cargas y los dos potenciales (indicando si alguno es nulo) en las configuraciones siguientes:

1. El conductor “1” está conectado a una fuente de tensión V₀ > 0 y el “2” está aislado y descargado.
2. El conductor “1” a una tensión V₀ > 0 y el “2” puesto a tierra.
3. El conductor “1” almacena una carga Q₀ > 0 y el “2” está aislado y descargado.
4. El conductor “1” almacena una carga Q₀ > 0 y el “2” está a tierra.

2 Introducción

Estos cuatro casos obedecen al mismo esquema: tenemos dos conductores de forma arbitraria en equilibrio electrostático. Por estar en equilibrio, estos conductores estarán a un cierto potencial y almacenará cierta carga. Se trata de, haciendo razonamientos generales, establecer el signo de alguna de las magnitudes, conocido el de otras.

Estas cantidades se relacionan por la ecuación matricial

En todos los casos existen dos (o más) procedimientos alternativos:

Analizar la dirección de las líneas de campo

• Las líneas de campo van de mayor a menor potencial, por tanto, si una línea va de un conductor 1 a un conductor 2, el potencial V₁ será mayor que V₂.
• Si de un conductor una línea de campo va hacia al infinito, el potencial del conductor será positivo; si viene de él, será negativo.
• Las líneas de campo electrostático no pueden formar bucles cerrados. No puede haber una línea que salga de un conductor y vuelva a él. Si una línea va del conductor 1 al 2, no puede haber otra que vaya del 2 al 1, ni directa ni indirectamente (pasando por el infinito).
• Si en la superficie de un conductor todas las líneas de campo van hacia afuera, su carga es positiva; si van hacia adentro, es negativa.
• Si el conductor posee carga nula habrá líneas que entren y líneas que salgan.

Estudiar el circuito equivalente

Para un sistema de dos conductores podemos construir un circuito equivalente formado por dos nodos, tres condensadores y una o dos fuentes (de tensión o de carga). Las capacidades de los condensadores de este circuito son todas positivas (o nulas). Las relaciones entre cargas y potenciales, en términos de las capacidades y autocapacidades son

Esto permite determinar los signos de cargas y potenciales.

Veámoslo para los cuatro casos indicados.

3 Primer caso

3.1 Por las líneas de campo

El conductor 1 tiene un potencial mayor que el del infinito (que es tierra), por lo que habrá líneas de campo que salen del 1 y van al infinito. Nos preguntamos entonces si habrá líneas que vayan del 2 al 1, o del 1 al 2 (no pueden darse las dos cosas a la vez).

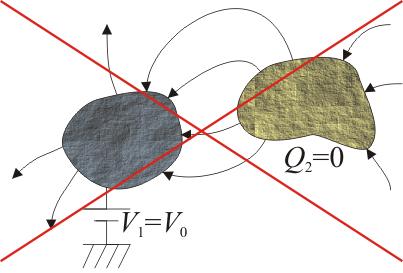
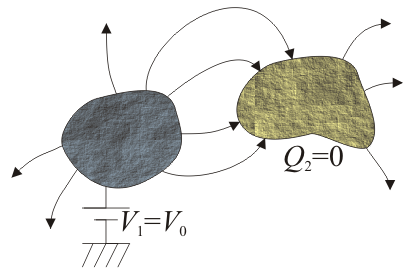
El conductor 2 está aislado y descargado, por lo que el flujo del campo eléctrico a través de una superficie que lo envuelva es nulo; esto quiere decir que por cada línea de campo que salga de 2 debe haber otra que entre. Si hay una línea de 2 que va a 1, debe haber otra que venga del infinito y entre en 2. Pero esto es imposible, porque tendríamos líneas cerradas en el ciclo .

Por tanto, las líneas deben ir de 2 a 1 y no al revés.

Entonces, tenemos que todas las líneas que tocan 2 van hacia afuera, el flujo del campo es positivo y [tex]Q_2>0[/tex]. Por otro lado, como hay líneas que van de 2 a 1, debe haberlas de 1 al infinito. Por tanto [tex]V_1 > 0[/tex].

3.2 Mediante el circuito equivalente

Este se compone de 2 nodos, tres condensadores y una fuente de tensión. Como el conductor 1 está aislado y descargado, no tenemos que conectar nada al nodo 1.

[center][img width=391 height=209]http://laplace.us.es/wiki/images/3/3b/Circuito-2amorfos-01.png[/img][/center]

Entonces el circuito equivalente se reduce a la asociación en paralelo de dos condensadores, uno de los cuales es la asociación en serie de otros 2. La capacidad equivalente del sistema será

[center][tex]C_\mathrm{eq}=\overline{C}_{22}+\frac{\overline{C}_{12}\overline{C}_{11}}{\overline{C}_{12}+\overline{C}_{11}}[/tex][/center]

y es positiva. Por tanto la carga del conductor 2 es

[center][tex]Q_2 = C_\mathrm{eq}V_0 > 0[/tex][/center]

mientras que la tensión del nodo 1, intermedio entre el 2 y tierra debe ser necesariamente positiva

[center][tex]V_1 = \frac{Q}{\overline{C}_{11}}=\frac{C_\mathrm{eq}}{\overline{C}_{11}}V_0 > 0[/tex][/center]

4 Segundo caso

5 Tercer caso

6 Cuarto caso