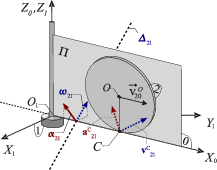
Disco contenido en un plano que rota (G.I.A.)
De Laplace
Contenido |
1 Enunciado
Un plano vertical Π ( sólido "0"), gira alrededor del eje vertical fijo O1Z1 con su eje O1X0 siempre contenido en el plano horizontal fijo O1X1Y1 ( sólido "1"), estando caracterizado dicho movimiento por el vector rotación 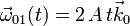 . Un disco de centro O y radio R (sólido "2"), contenido en todo instante en el plano Π, rueda sin deslizar sobre el eje horizontal O1X0, siendo la velocidad relativa de su centro
. Un disco de centro O y radio R (sólido "2"), contenido en todo instante en el plano Π, rueda sin deslizar sobre el eje horizontal O1X0, siendo la velocidad relativa de su centro 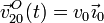 (con v0 constante). Si en el instante inicial (t = 0), el centro O se encontraba en el eje O1Z1, determina:
(con v0 constante). Si en el instante inicial (t = 0), el centro O se encontraba en el eje O1Z1, determina:
- Los vectores velocidad angular
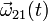 y aceleración angular
y aceleración angular 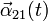 en un instante cualquiera.
en un instante cualquiera.
- Los vectores aceleración
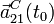 en un instante t = t0 en el que el punto C del disco se halla en contacto con el plano horizontal O1X1Y1.
en un instante t = t0 en el que el punto C del disco se halla en contacto con el plano horizontal O1X1Y1.
- El eje instantáneo de rotación y mínimo deslizamiento del movimiento {21} en el citado instante t = t0.
2 Solución
Los datos cinemáticos proporcionados por el problema son la velocidad angular del sólido "0" respecto al "1" y la velocidad del punto O perteneciente al sólido "2" moviéndose respecto al sólido "0". Expresados en los ejes propuestos en la figura son
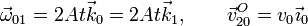
2.1 Movimiento {01}
Este movimiento es de rotación permanente del plano Π alrededor del eje O1Z1 con velocidad angular dependiente del tiempo. Tenemos
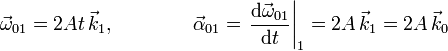
Al ser una rotación de eje permanente, cualquier punto del eje tiene velocidad y aceleración nulas. Si escogemos el origen del sistema O1, la reducción del movimiento y las aceleraciones son, expresadas en la base del sólido "0"
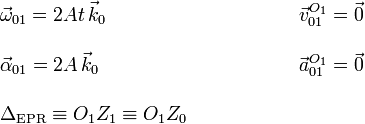
Calculamos la velocidad 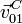 en el instante t = t0 en que
está tocando el eje OX0. Dado que en t = 0 el centro del disco O
estaba en el eje O1Z1, y la velocidad de traslación del centro del
disco sobre el eje OX0 es constante e igual a v0, en el instante
t0 la distancia entre los puntos O1 y C es v0t0, por lo
que se tiene
en el instante t = t0 en que
está tocando el eje OX0. Dado que en t = 0 el centro del disco O
estaba en el eje O1Z1, y la velocidad de traslación del centro del
disco sobre el eje OX0 es constante e igual a v0, en el instante
t0 la distancia entre los puntos O1 y C es v0t0, por lo
que se tiene
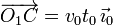
Utilizando las ecuaciones del campo de velocidades y aceleraciones del movimiento {01} obtenemos
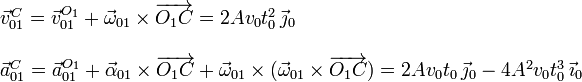
2.2 Movimiento {20}
Dado que el disco rueda sin deslizar, la velocidad
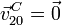 . Es decir, el eje instantáneo de este
movimiento pasa por el punto C. Por otro lado, el eje de giro es
perpendicular al plano Π, es decir, se tiene
. Es decir, el eje instantáneo de este
movimiento pasa por el punto C. Por otro lado, el eje de giro es
perpendicular al plano Π, es decir, se tiene
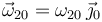 . Para determinar ω20 usamos el
dato de la velocidad del punto C en el movimiento {20}. Tenemos
. Para determinar ω20 usamos el
dato de la velocidad del punto C en el movimiento {20}. Tenemos

Por otro lado, la aceleración del punto O es

Esta derivada puede hacerse suponiendo que 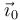 es constante, pues
la expresión de
es constante, pues
la expresión de 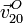 en la base vectorial del sólido "0" es
válida para todo t. Usando el mismo argumento para derivar
en la base vectorial del sólido "0" es
válida para todo t. Usando el mismo argumento para derivar
 podemos caracterizar completamente el movimiento
podemos caracterizar completamente el movimiento
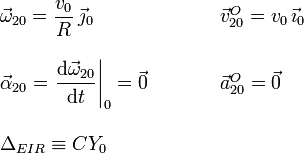
La velocidad y aceleración en el punto C son
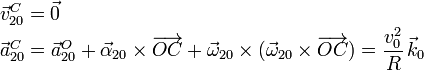
2.3 Movimiento {21}
Usando las reglas de composición de movimientos obtenemos
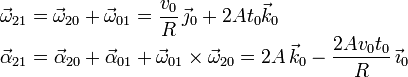
Para la velocidad y aceleración, tenemos
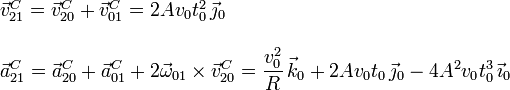
EL vector de posición de un punto del eje instantáneo del movimiento {21} puede calcularse respecto al punto C
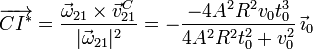
Tomando como referencia el origen de coordenadas, la ecuación paramétrica del eje es
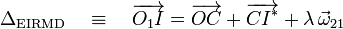
La velocidad mínima es
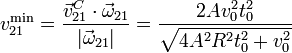
Por tanto, el movimiento es helicoidal tangente. La figura muestra aproximadamente las magnitudes cinemáticas más relevantes.