Problemas de movimiento relativo (G.I.T.I.)
De Laplace
Contenido |
1 Comparación de velocidades relativas de dos sólidos
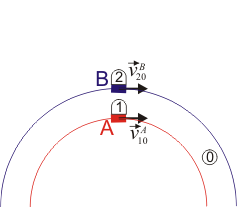
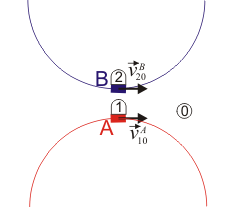
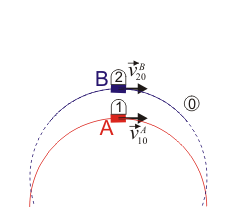
Se tienen dos vagonetas A y B (sólidos “1” y “2”), que avanzan por raíles sobre el suelo horizontal (sólido “0”). En un momento dado las vagonetas se mueven paralelamente respecto al suelo con velocidades
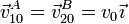
El vector de posición relativo entre las dos vagonetas es
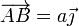
Los ejes de los tres sistemas se toman paralelos de forma que los vectores de las respectivas bases son coincidentes en ese instante.
Halle las velocidades relativas
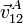y 
en los siguientes casos:
- Las vagonetas se mueven por vías rectilíneas paralelas.
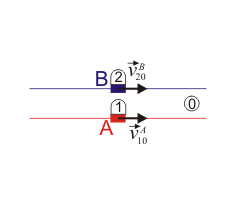
- La vagoneta A se mueve por una vía circular de radio R, mientras que B se mueve por una vía rectilínea. El instante descrito es el de máximo acercamiento entre las dos vías.
- Las dos se mueven por vías circulares concéntricas, de radios R y R + a, respectivamente.
- Las dos se mueven por arcos de circunferencia de radio R con centros en lados opuestos
- Las dos se mueven por arcos de circunferencia de radio R con centros hacia el mismo lado
| 
| 
|
| (1) | (2) | (3) |
|---|---|---|
| 
| |
| (4) | (5) |
- Si además suponemos que los movimientos de las dos vagonetas son uniformes, calcule las aceleraciones relativas
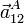y 
para los casos anteriores.
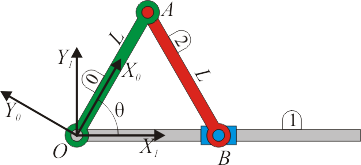
2 Movimiento relativo de un sistema biela-manivela
Se tiene un sistema biela-manivela formado por dos barras de longitud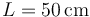 
. La manivela (sólido “0”) gira alrededor de un punto O, extremo de una barra (sólido 1) que podemos considerar fija. La biela (sólido “2”) está articulada a la manivela en un punto A, mientras que su otro extremo B está obligado a deslizar sobre la barra “1”.
En un instante dado la manivela forma con la barra un ángulo tal que tg(θ) = 4 / 3 . En el mismo instante las derivadas de este ángulo valen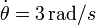 
, 
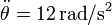. Para
este instante:
- Calcule las velocidades ,
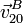y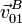 
. Indique su dirección y sentido gráficamente.
- Halle las aceleraciones ,
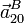y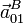 
.
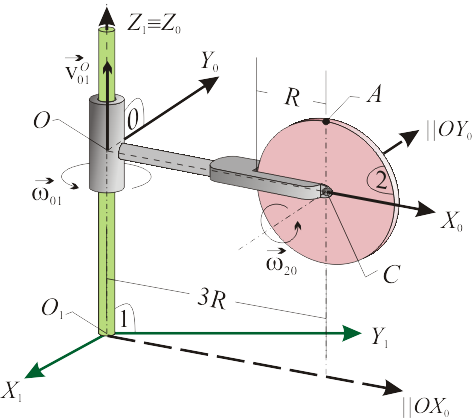
3 Disco con eje en vástago
El sólido rígido 0 del mecanismo de la figura se corresponde con un vástago OC de longitud 3R que, mediante un par cilíndrico situado en su extremo O, permanece en todo instante perpendicular al eje vertical fijo O1Z1 (sólido 1). Dicho par de enlace permite que el vástago gire alrededor de O1Z1 con velocidad angular constante de módulo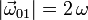 
y en el sentido mostrado en la figura; a su vez, el extremo O se desplaza sobre el eje vertical O1Z1 en sentido positivo y con velocidad constante, siendo el módulo de ésta 
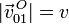. El extremo C del sólido “0” está articulado al centro de un disco de radio R (sólido “2”), siempre contenido en el plano vertical OX0Z0; el movimiento relativo del disco respecto del vástago consiste en una rotación permanente alrededor de un eje paralelo a OY0 que pasa por C, en el sentido indicado en la figura y con velocidad angular constante cuyo módulo es 
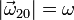. Utilizando la base vectorial del triedro ligado al sólido 0, OX0Y0Z0, para expresar las magnitudes vectoriales,
determine:
- El vector velocidad angular
y el vector aceleración angular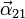 
, correspondientes al movimiento del disco respecto al triedro fijo.
- Las velocidades del punto A del perímetro del disco en el instante en que aquél ocupa el extremo más alto del diámetro vertical (ver figura), para cada uno de los tres movimientos relativos que se distinguen en el mecanismo descrito:
, 
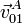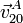y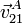 
.
- Las aceleraciones
, 
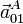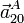y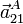 
para el mismo punto y en el mismo instante especificado en el apartado anterior.
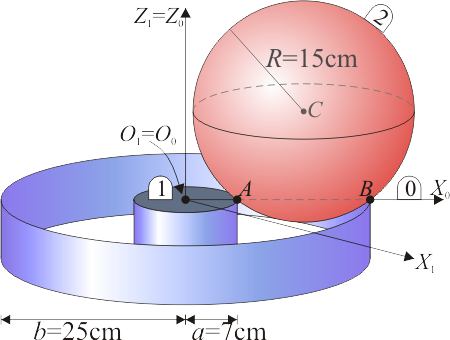
4 Bola en canal circular
Una bola de radio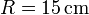 
(sólido “2”), se desplaza sobre dos carriles circulares concéntricos fijos de radio interior 
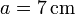y exterior 
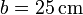(sólido “1”), situados en un plano horizontal (ver figura). El movimiento de esta esfera es tal que:
- en todo instante, rueda sin deslizar sobre ambos carriles, y
- su centro C realiza un movimiento circular uniforme con celeridad
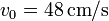y en sentido antihorario respecto al eje OZ.
Consideramos como sólido móvil intermedio (sólido 0) al plano O1X0Z0 que contiene en todo instante al centro C de la esfera (ver figura).
- Halle los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
- Halle la reducción canónica (o reducción cinemática) en cada caso.
- Para el punto de la pelota en contacto con el carril de mayor diámetro (punto B), determine
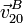y .
5 Rotación de un disco inclinado
Un disco de radio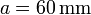 
en cuyo eje está ensartada una barra de longitud 
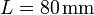se halla apoyada en el extremo de la barra y en el borde del disco. El disco rueda sobre una superficie horizontal, manteniendo fija la posición del extremo de la barra. El giro es uniforme, de forma que el centro del disco completa una revolución cada 
.
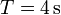Se consideran como sólido 1 la superficie horizontal, como sólido intermedio 0 uno que gira alrededor del eje Z, de forma que la barra se encuentra permanentemente en el plano XZ y como sólido 2 el disco. En un instante dado de toman los ejes del sistema 0 y 1 coincidentes y tales que OZ es la normal al plano horizontal que pasa por O, el extremo de la barra, OX es la recta horizontal que pasa por O y por A, el punto de contacto del disco con la mesa, y OY es la normal a los otros dos ejes.
- Determine la posición de los ejes instantáneos de rotación en los movimientos absoluto {21}, relativo {20} y de arrastre {01}.
- Halle las velocidades de los puntos A (de contacto del disco con la mesa), B (diametralmente opuesto a A) y C (centro del disco), en los tres movimientos.
- Calcule la aceleración de los mismos puntos.
- Suponga que se marca un punto en el borde del disco y se analiza su movimiento a lo largo del tiempo. ¿Es éste periódico? Si es así, ¿cuál es su periodo?
