Parámetro arco de una hélice (G.I.A.)

De Laplace

Revisión a fecha de 10:53 2 nov 2010; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Sea la hélice $Γ$ descrita en un sistema de referencia cartesiano $O X Y Z$ por las siguientes ecuaciones paramétricas:

$\Gamma\,:\,\vec{r} = \vec{r}(\lambda) \left\{ \begin{array}{l} x(\lambda) = a \cos\lambda\\ y(\lambda) = a \,\mathrm{sen}\,\lambda\\ z(\lambda) = a \lambda \end{array} \right.$

donde $a$ y $h$ son constantes conocidas.

Determina el parámetro arco de la hélice descrita.
Obtén los vectores del triedro intrínseco en cada punto de dicha curva.
Calcula su radio de curvatura.

2 Solución

El diferencial del parámetro natural es el módulo del desplazamiento elemental

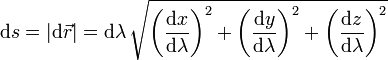
$\mathrm{d}s=|\mathrm{d}\vec{r}| =\mathrm{d}\lambda\, \sqrt{\left(\dfrac{\mathrm{d}x}{\mathrm{d}\lambda}\right)^2+ \left(\dfrac{\mathrm{d}y}{\mathrm{d}\lambda}\right)^2+ \left(\dfrac{\mathrm{d}z}{\mathrm{d}\lambda}\right)^2}$

Derivando en la ecuación paramétrica de la curva obtenemos

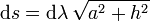
$\mathrm{d}s=\mathrm{d}\lambda\,\sqrt{a^2+h^2}$

Integrando en ambos lados obtenemos

$s = \lambda\,\sqrt{a^2+h^2} + A$

donde $A$ es una constante. Podemos fijar su valor imponiendo $s = 0$ cuando $λ = 0$ . Esto es simplemente cambiar el punto inicial de la curva. Así pues el parámetro arco es

$s = \lambda\,\sqrt{a^2+h^2}$

Reparametrizamos la ecuación vectorial de la curva

$\Gamma\,:\,\vec{r} = \vec{r}(s) \left\{ \begin{array}{l} x(s) = a \cos\left(\dfrac{s}{\sqrt{a^2+h^2}} \right)\\ \\ y(s) = a \,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}} \right)\\ \\ z(s) = \dfrac{hs}{\sqrt{a^2+h^2}} \end{array} \right.$

Ahora podemos calcular el triedro intrínseco de forma sencilla.

El vector tangente es

$\vec{T} = \vec{r}\,' = \left[ -\dfrac{a}{\sqrt{a^2+h^2}}\,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}} \right), \dfrac{a}{\sqrt{a^2+h^2}}\cos\left(\dfrac{s}{\sqrt{a^2+h^2}} \right), \dfrac{h}{\sqrt{a^2+h^2}} \right]$

Podemos comprobar que $|\vec{r}\,'|=1$ , dado que $\vec{r}$ está expresado en el parámetro arco.

El vector normal es

$\vec{N} = \dfrac{\vec{T}'}{|\vec{T}'|} = \left[ -\cos\left(\dfrac{s}{\sqrt{a^2+h^2}}\right), -\,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}}\right), 0 \right]$

Y el vector binormal es

$\vec{B} = \vec{T}\times\vec{N} = \left[ \dfrac{h}{\sqrt{a^2+h^2}}\,\mathrm{sen}\,\left(\dfrac{s}{\sqrt{a^2+h^2}} \right), -\dfrac{h}{\sqrt{a^2+h^2}}\cos\left(\dfrac{s}{\sqrt{a^2+h^2}} \right), \dfrac{a}{\sqrt{a^2+h^2}} \right]$

Por definición, el radio de curvatura es

$R_{\kappa}=\dfrac{1}{\kappa}=\dfrac{1}{|\vec{T}'|} = \dfrac{a^2+h^2}{a}$

Es interesante observar que si $h = 0$ reobtenemos el radio de curvatura de una circunferencia.

Parámetro arco de una hélice (G.I.A.)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES