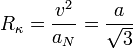Barra girando en un plano (G.I.A.)
De Laplace
Contenido |
1 Enunciado
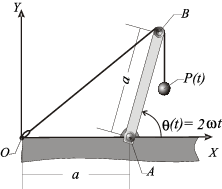
Una barra rígida AB de longitud 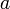 se mueve en un plano
vertical OXY, manteniendo su extremo A articulado en un punto
del eje horizontal de coordenadas
se mueve en un plano
vertical OXY, manteniendo su extremo A articulado en un punto
del eje horizontal de coordenadas 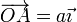 , y
verificando la ley horaria θ(t) = 2ωt, con
, y
verificando la ley horaria θ(t) = 2ωt, con 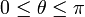 y siendo ω = cte. Un hilo inextensible de
longitud 2a tiene uno de sus extremos conectado al origen del
sistema de referencia (punto O), mientras que del otro cuelga
una partícula P que mantiene al hilo siempre tenso. El hilo se
apoya sobre una pequeña polea de radio despreciable situada en el
extremo B de la barra, de forma que el tramo
y siendo ω = cte. Un hilo inextensible de
longitud 2a tiene uno de sus extremos conectado al origen del
sistema de referencia (punto O), mientras que del otro cuelga
una partícula P que mantiene al hilo siempre tenso. El hilo se
apoya sobre una pequeña polea de radio despreciable situada en el
extremo B de la barra, de forma que el tramo 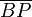 permanece siempre paralelo al eje OY (ver figura). Se pide:
permanece siempre paralelo al eje OY (ver figura). Se pide:
- Ecuaciones horarias del punto
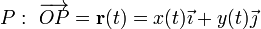 .
.
- Instante del tiempo tM en que la partícula alcanza su altura máxima.
- Radio de curvatura de la trayectoria seguida por P, en el instante considerado en el apartado anterior.
2 Solución
2.1 Ecuaciones horarias del punto 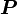
Podemos construir el vector  como
como
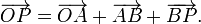
Veamos como calcular cada uno de los vectores
El vector  es simplemente el vector de posición del punto
A
es simplemente el vector de posición del punto
A
![\overrightarrow{OA} = [a,0,0]](/wiki/images/math/0/5/f/05f2a10955398266f307c6e6f502392d.png)
Calculamos las componentes de 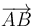 proyectando sobre los ejes a
través del ángulo θ
proyectando sobre los ejes a
través del ángulo θ
![\overrightarrow{AB} = [a\cos\theta,a\,\mathrm{sen}\,\theta,0]](/wiki/images/math/a/7/b/a7b20e3fa89a46fc196c14233426f0ba.png)
Por último el vector 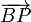 es
es
![\overrightarrow{BP} = -|\overrightarrow{BP}|\,\vec{\jmath} = [0,-|\overrightarrow{BP}|,0]](/wiki/images/math/1/9/1/19114d83a0bf23d8108fa7e63591a931.png)
Sabiendo que la longitud total del hilo es 2a, del dibujo vemos que
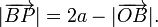
Tenemos 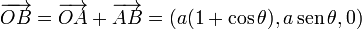 , luego
su módulo es
, luego
su módulo es
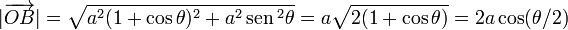
donde hemos usado 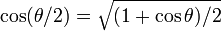 . Entonces
. Entonces
![\overrightarrow{BP} = [0,-2a(1-\cos(\theta/2)),0]](/wiki/images/math/8/8/3/88370c19c7baeef9ba7e3bdf78ae1850.png)
A partir de la expresión de  obtenemos
obtenemos
![\overrightarrow{OP} = [ a(1+\cos\theta),a(\,\mathrm{sen}\,\theta-2 +2\cos(\theta/2)),0]](/wiki/images/math/b/5/2/b523bb99f7623f6658fba9b80da14205.png)
Sustituyendo la ley horaria θ(t) = 2wt obtenemos
![\overrightarrow{OP}(t) = [ a(1+\cos(2wt)),a(\,\mathrm{sen}\,(2wt)-2+2\cos(wt)),0]](/wiki/images/math/7/e/5/7e550fc6b6152ddb94ab34b1ad4f846b.png)
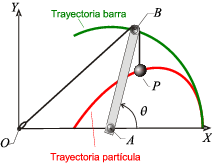
El dibujo indica la trayectoria seguida por el punto P y el extremo de la barra B
2.2 Instante en que alcanza la altura máxima
La partícula alcanza su altura máxima cuando la componente Y de la velocidad se anula. La velocidad de la partícula es
![\begin{array}{ll}
\vec{v}_P = \dot{\overrightarrow{OP}} =&
[-2aw\,\mathrm{sen}\,(2wt),2aw(\cos(2wt)-\,\mathrm{sen}\,(wt)),0] =\\
& [-2aw\,\mathrm{sen}\,(\theta),2aw(\cos(\theta)-\,\mathrm{sen}\,(\theta/2)),0]
\end{array}](/wiki/images/math/e/a/3/ea3454a0b2638dad100e73c8448e6a60.png)
Para que la velocidad vy sea nula debe ocurrir que
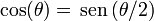
Teniendo en cuenta que 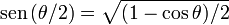 ,
elevando al cuadrado llegamos a la ecuación
,
elevando al cuadrado llegamos a la ecuación
Esta ecuación tiene dos soluciones
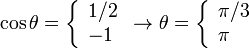
El punto de altura máxima corresponde al primer valor. Así pues el ángulo para el que la altura es máxima, y el tiempo correspondiente son

2.3 Radio de curvatura en 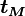
Necesitamos la aceleración en el instante tM. La aceleración en cualquier instante es
![\begin{array}{ll}
\vec{a}_P = \dot{\vec{v}}_P =&
[-4aw^2\cos(2wt),-2aw^2(-2\,\mathrm{sen}\,(2wt)+\cos(wt)),0] =\\
&[-4aw^2\cos(\theta),-2aw^2(2\,\mathrm{sen}\,(\theta)+\cos(\theta/2)),0]
\end{array}](/wiki/images/math/0/9/0/090251df0b17dec8c47270b4f67edefa.png)
En el instante tM la velocidad y la aceleración son
![\begin{array}{l}
\vec{v}_P(t_M) = [-\sqrt{3}aw,0,0]\\
\vec{a}_P(t_M) = [-2aw^2,-3\sqrt{3}a w^2,0]
\end{array}](/wiki/images/math/c/f/9/cf99e52ad9ecf7e93fc178724d386f64.png)
La componente normal de la aceleración es
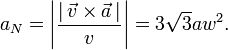
Y el radio de curvatura es