Tiro oblicuo (G.I.A.)

De Laplace

Revisión a fecha de 09:33 2 nov 2010; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Determina el movimiento de un proyectil disparado con una velocidad inicial $v 0$ y un ángulo $α$ con la horizontal. El proyectil está sometido a la acción de la gravedad. Calcula el radio de curvatura en el punto más alto de su trayectoria.

2 Solución

El campo gravitatorio ejerce una fuerza 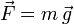$\vec{F}=m\,\vec{g}$ sobre una partícula de masa $m$ . Según la Segunda Ley de Newton la aceleración de la partícula es

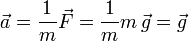
$\vec{a} = \dfrac{1}{m}\vec{F} = \dfrac{1}{m}m\,\vec{g} = \vec{g}$

El enunciado nos da un sistema de ejes en el que la aceleración de la gravedad está dirigida en el sentido negativo del eje $O Z$ , esto es

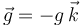
$\vec{g} = -g\,\vec{k}$

La velocidad de la partícula se calcula como la integral del vector aceleración en el tiempo. Si la velocidad inicial es $\vec{v}(0)$ tenemos

$\int\limits_{\vec{v}(0)}^{\vec{v}(t)}\mathrm{d}\vec{v} = \int\limits_0^t\vec{a}\,\mathrm{d} t \Longrightarrow \vec{v}(t) = \vec{v}(0) - \int\limits_0^t g\,\vec{k}\,\mathrm{d} t$

Teniendo en cuenta que $g$ y $\vec{k}$ son constantes podemos hacer la integral para obtener

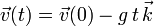
$\vec{v}(t) = \vec{v}(0) - g\,t\,\vec{k}$

La posición se determina de modo similar integrando la velocidad

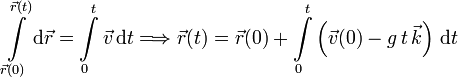
$\int\limits_{\vec{r}(0)}^{\vec{r}(t)}\mathrm{d}\vec{r} = \int\limits_0^t \vec{v} \,\mathrm{d} t \Longrightarrow \vec{r}(t) = \vec{r}(0) + \int\limits_0^t\left(\vec{v}(0) - g\,t\,\vec{k} \right)\,\mathrm{d} t$

Como $\vec{v}(0)$ , $g$ y $\vec{k}$ son constantes obtenemos

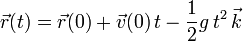
$\vec{r}(t) = \vec{r}(0) + \vec{v}(0)\,t - \dfrac{1}{2}g\,t^2\,\vec{k}$

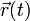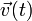Las expresiones para $\vec{r}(t)$ y $\vec{v}(t)$ describen el movimiento genérico de una partícula en el seno del campo gravitatorio. El movimiento concreto depende del valor de estas condiciones iniciales. Vamos a ver los tres casos descritos en el enunciado.

Tiro oblicuo (G.I.A.)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES