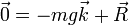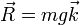Dinámica del punto material (G.I.T.I.)

De Laplace

Revisión a fecha de 17:34 7 oct 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Introducción

2 Principios de la Dinámica

Los principios de la dinámica o Leyes de Newton son los axiomas por los que se rigen las partículas y sistemas en la dinámica clásica. Fueron enunciados por Newton, basándose en los trabajos de Galileo, en sus Principia Mathematica.

Una versión de estos principios, enunciada de forma moderna, es la siguiente, donde encabezamos cada principio con el nombre con el que se lo conoce habitualmente:

2.1 Primer principio: Principio de inercia

El primer principio de la dinámica, también conocido como Primera Ley de Newton puede formularse como

“Toda partícula libre de interacciones permanece en reposo o en estado de movimiento rectilíneo y uniforme.”

Normalmente se formula usando “fuerzas” en lugar de “interacciones” pero puesto que ello requiere el haber definido previamente el concepto de fuerza, es preferible enunciarlo de una manera más genérica.

Este principio fue enunciado inicialmente por Galileo.

Lo que nos dice esta ley es que el espacio es euclídeo ya que las trayectorias de las partículas libres son rectas y no circunferencias (como ocurriría en la superficie de una esfera). El primer principio de la dinámica nos permite definir los sistemas de referencia inerciales como aquellos en que una partícula libre sigue un movimiento rectilíneo y uniforme.

El principio de inercia se ve modificado en la teoría general de la relatividad, que corrige y generaliza las leyes de Newton.

2.1.1 Sistemas de referencia inerciales

2.2 Segundo principio: Segunda Ley de Newton

El segundo principio de la dinámica requiere previamente la definición de la cantidad de movimiento 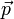$\vec{p}$ de una partícula, como

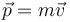
$\vec{p}=m\vec{v}$

de manera que la ley se enuncia

“La derivada de la cantidad de movimiento de una partícula es igual a la resultante de las fuerzas aplicadas sobre ella.”

En forma matemática

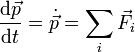
$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=\dot{\vec{p}} = \sum_i \vec{F}_i$

En la mayoría de las ocasiones, la masa de una partícula es una constante por lo que la derivada de la cantidad de movimiento es igual a

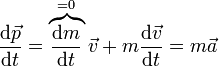
$\frac{\mathrm{d}\vec{p}}{\mathrm{d}t} = \overbrace{\frac{\mathrm{d}m}{\mathrm{d}t}}^{=0}\vec{v}+m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} = m \vec{a}$

de donde llegamos a la forma habitual de expresar la segunda ley de Newton

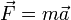
$\vec{F}=m\vec{a}\,$

con $\vec{F}$ la resultante de las fuerzas aplicadas sobre la partícula, hallada como suma vectorial de ellas.

Principio de superposición: Si sobre un mismo punto material actúan dos fuerzas simultáneamente, la aceleración que adquiere es la suma vectorial de las aceleraciones que le comunicarían cada una de las dos fuerzas por separado.; También se conoce a éste como principio de independencia de acción de las fuerzas, y se puede generalizar para un número arbitrario, de fuerzas.

La segunda ley de Newton implica que la aceleración que adquiere una partícula es proporcional a la fuerza neta aplicada sobre ella, siendo la constante de proporcionalidad, $m$ , una propiedad de cada partícula, conocida como masa inercial.

Esta ley requiere el conocimiento de las fuerzas aplicadas, como un dato del problema. Estas fuerzas deben ser obtenidas independientemente para que la ley tenga verdadero significado. Por ello, precisamos de algún modelo físico que nos proporcione la expresión de la fuerza. Entre estos modelos se encuentran:

La ley de Hooke, para el oscilador armónico

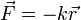
$\vec{F}=-k\vec{r}\,$

La ley de la gravitación universal, para el movimiento de una masa en el campo gravitatorio de otra

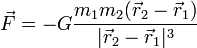
$\vec{F}=-G\frac{m_1m_2(\vec{r}_2-\vec{r}_1)}{|\vec{r}_2-\vec{r}_1|^3}$

Esta ley contiene al caso particular e importante del movimiento de una masa pequeña en las proximidades de la superficie terrestre

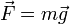
$\vec{F}=m\vec{g}\,$

La ley de Lorentz, para el movimiento de una partícula en un campo electromagnético

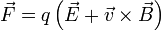
$\vec{F}=q\left(\vec{E}+\vec{v}\times\vec{B}\right)\,$

Un caso particular de esta ley es la ley de Coulomb, para la fuerza producida por una carga en reposo

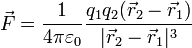
$\vec{F}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2(\vec{r}_2-\vec{r}_1)}{|\vec{r}_2-\vec{r}_1|^3}$

Una característica común a todas estas leyes de fuerza es que proporcionan una fuerza dependiente de la posición y de la velocidad instantáneas de la partícula.

2.3 Tercer principio: ley de acción y reacción

Los dos primeros principios de la dinámica nos dicen cómo se comportan las partículas en ausencia de fuerzas o sometidas a una fuerza conocida. El tercer principio de la dinámica establece una propiedad básica de esas fuerzas de interacción entre partículas:

“Si una partícula A ejerce en un instante dado una fuerza sobre una partícula B, la partícula B ejerce sobre A una fuerza igual y de sentido contrario.”

Matemáticamente

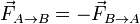
$\vec{F}_{A\to B} = -\vec{F}_{B\to A}$

Hay que destacar que estas dos fuerzas no se anulan mutuamente, ya que se ejercen sobre partículas distintas. Sólo en el caso de que se encuentren rígidamente unidas se cancelarán sus efectos.

Ambas fuerzas actúan simultáneamente. Por ello, hay que señalar que el nombre de “acción y reacción”, con el que se conoce habitualmente a esta ley, es engañoso en cuanto a que sugiere a que primero actúa la acción y posteriormente la reacción. No es así y no existe distinción alguna que convierta a una de las fuerzas en acción y a la otra en reacción.

La tercera ley de Newton puede formularse en dos versiones. La versión débil es la enunciada más arriba, donde solo indica que las fuerzas son iguales y opuestas. La versión fuerte es más restrictiva e informativa:

“Si una partícula A ejerce en un instante dado una fuerza sobre una partícula B, la partícula B ejerce sobre A una fuerza igual y de sentido contrario y ambas fuerzas actúan sobre la recta que pasa por las dos partículas”

Matemáticamente

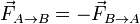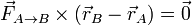
$\vec{F}_{A\to B} = -\vec{F}_{B\to A}$ y $\vec{F}_{A\to B}\times(\vec{r}_B-\vec{r}_A)=\vec{0}$

Este requisito adicional establece que las fuerzas de interacción son centrales, lo que tiene importantes consecuencias en la ley de conservación del momento cinético de un sistema de partículas.

No todas las fuerzas de la naturaleza cumplen la tercera ley de Newton. Las que sí lo hacen se denominan fuerzas newtonianas. Entre las fuerzas newtonianas se encuentran los ejemplos importantes de la ley de la gravitación universal, la ley de Hooke y la ley de Coulomb, por lo que las consecuencias del principio de acción y reacción se aplican a la mayoría de los casos prácticos.

3 El problema fundamental de la dinámica

La segunda ley de Newton relaciona la segunda derivada de la posición con la fuerza que actúa sobre la partícula

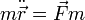
$m\ddot{\vec{r}}=\vec{F}m$

De acuerdo con esta ecuación, si conocemos la posición de una partícula como función del tiempo, podemos determinar la fuerza que actúa sobre ella. Este es el principio que se usa en un dinamómetro. Sabiendo el estado de movimiento (o de reposo, en el caso estático), empleamos este dato para medir la fuerza.

No obstante, no es este el problema principal en dinámica.

El problema fundamental de la dinámica es: conocida la fuerza que actúa sobre una partícula, así como su posición y velocidad iniciales, ¿cómo se mueve dicha partícula?

En el caso de que conozcamos la fuerza como función del tiempo, la respuesta es sencilla: basta con integrar dos veces respecto al tiempo

$\vec{v}(t) = \vec{v}_0 + \int_0^t\frac{\vec{F}(t')}{m}\,\mathrm{d}t'$ $\vec{r}(t) = \vec{r}_0+\int_0^t\vec{v}(t')\,\mathrm{d}t'$

Lo normal, sin embargo, es que la fuerza no se conozca como función del tiempo, sino como función de la posición (por ejemplo, de acuerdo con la ley de Hooke, la fuerza ejercida por un resorte es $F = - k x$ ), de la velocidad (por ejemplo, la fuerza de Coriolis, que aparece en un sistema no inercial, es proporcional a la velocidad) y en ocasiones del tiempo, esto es

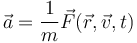
$\vec{a}=\frac{1}{m}\vec{F}(\vec{r},\vec{v},t)$

o, en términos de las derivadas de la posición

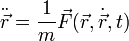
$\ddot{\vec{r}}=\frac{1}{m}\vec{F}(\vec{r},\dot{\vec{r}},t)$

Esto quiere decir que para poder determinar la posición como función del tiempo, debemos integrar una función... que no conocemos hasta que hayamos determinado la propia posición. Esta aparente circularidad convierte a esta fórmula en lo que se conoce como una ecuación diferencial y hace que su integración no sea absoluto trivial. De hecho, en solo algunos casos es posible determinar analíticamente la posición incluso aunque se conozca perfectamente la fuerza.

En numerosas situaciones de interés, es preciso recurrir a la integración numérica, en la cual se obtiene la posición, con una cierta precisión, con ayuda de ordenadores. Por ejemplo, el movimiento de la Tierra respecto al Sol puede determinarse exactamente, si solo consideramos estos dos astros, pero el movimiento del sistema Tierra-Luna alrededor del Sol es imposible de resolver analíticamente y requiere de técnicas aproximadas.

El problema se agrava porque a menudo el conocimiento de la fuerza es incompleto. Se conocen algunas fuerzas aplicadas sobre la partícula, pero otras son también incógnitas del problema. En particular, las conocidas como fuerzas de reacción vincular, asociadas a la presencia de restricciones sobre el movimiento de la partícula (por ejemplo, para el caso de un péndulo, la tensión de la cuerda es una incógnita del problema).

Todo ello hace que el problema de la dinámica de una partícula (y no digamos el de un sistema de partículas interactuantes) sea uno de los más complicados de la Física y que solo algunos resultados parciales sean fácilmente accesibles.

4 Estática de la partícula

Artículo completo: Estática de la partícula

La estática es la parte de la mecánica que trata de las situaciones de equilibrio de los cuerpos. Un estado de equilibrio es aquél en el que el sistema se encuentra en reposo, permaneciendo en él indefinidamente.

El análisis del equilibrio de un sistema se compone de dos elementos:

Establecer las condiciones en las que se produce el estado del equilibrio
Establecer la estabilidad del equilibrio, esto es, determinar si el sistema, separado de su estado de equilibrio, vuelve a él o por el contrario se aleja de él.

4.1 Condición de equilibrio

Para el caso de una partícula material, la condición de equilibrio es una consecuencia inmediata de la segunda ley de Newton. Si la partícula se encuentra en un estado de reposo permanente, su aceleración es nula y por tanto

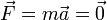
$\vec{F}=m\vec{a}=\vec{0}$

La condición de equilibrio de una partícula es que se anule la resultante de las fuerzas que actúan sobre ella.

Cuando tenemos fuerzas dependientes de la posición, este principio sirve para determinar las posiciones de equilibrio.

Por ejemplo, supongamos una masa sujeta a la acción de la gravedad y que cuelga de un resorte vertical, que verifica la ley de Hooke. Sumando las componentes verticales del peso y de la fuerza elástica tenemos que, en el equilibrio

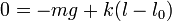
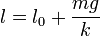
$0 = -mg + k(l-l_0)\,$ $\Rightarrow$ $l = l_0+\frac{mg}{k}$

Si lo que se conoce es la posición de equilibrio y parte de las fuerzas actuantes, la condición de equilibrio sirve para determinar la fuerza restante. Este es el principio de un dinamómetro estático. A partir de la deformación de un resorte, cuya ley de fuerza se conoce, es posible determinar la fuerza aplicada sobre la masa situada en su extremo.

4.2 Estabilidad del equilibrio

El que una posición sea de equilibrio no garantiza que, en una situación real, el sistema vaya a permanecer en ella indefinidamente. La razón es que siempre existen pequeñas fluctuaciones en las fuerzas, que pueden separar levemente al sistema del equilibrio. Para que el sistema permanezca en la misma posición, no basta con que su posición sea de equilibrio. Éste debe ser estable.

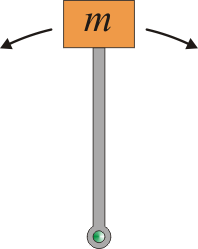
Consideremos, por ejemplo, un péndulo simple formado por una masa que cuelga de un punto de anclaje sujeto por una barra rígida sin masa. Este sistema posee dos posiciones de equilibrio: que la masa está en el punto más bajo del péndulo, o que esté en el punto más alto. Es claro que las dos posiciones no son equivalentes. Mientras que en la posición inferior la masa tiende a permanecer en ella, si se encuentra en el extremo superior cualquier pequeña perturbación hace que la masa caiga.

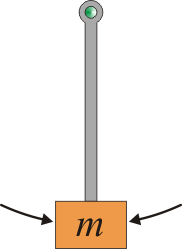
Estable	Inestable

Los puntos de equilibrio se clasifican en:

Estables: Ante una pequeña perturbación, tienden a retornar a la posición de equilibrio. El ejemplo representativo lo supone una partícula que rueda dentro de un cuenco, o una masa sujeta a un resorte.

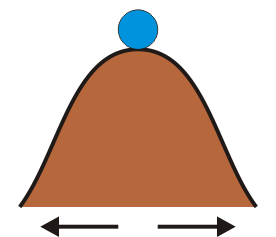
Inestables: Una pequeña perturbación aleja a la masa del equilibrio, y ésta tiende a alejarse de esta posición. Es el caso de una masa situada en lo alto de una cima. También es el caso de una anilla en el centro de una barra en rotación. Cuando se separa del centro, la fuerza centrífuga tiende a alejarla aun más.

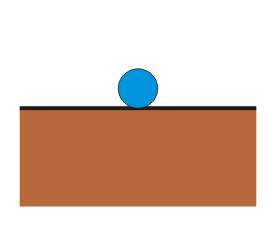
Indiferente: La partícula no tiende a retornar a la posición de equilibrio, pero tampoco a alejarse de ella. Es el caso de una bola situada sobre una mesa horizontal.

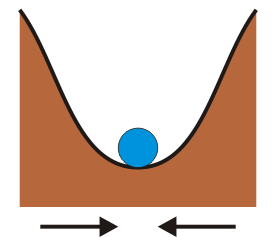
Estable	Inestable	Indiferente

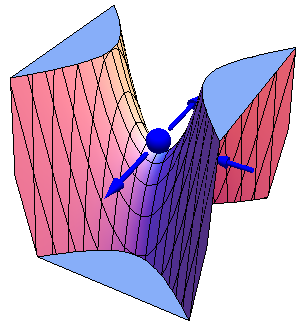
La clasificación se complica por el hecho de que una posición de equilibrio puede ser estable respecto a ciertas fuerzas e inestables frente a otras. Por ejemplo, en una superficie en forma de silla de montar la posición es de equilibrio estable en una dirección e inestable en la perpendicular.

La forma más directa de abordar el problema de la estabilidad consiste en suponer una posición muy próxima a la de equilibrio y analizar el sentido de la fuerza para un desplazamiento dado. Por ejemplo, en el caso del resorte que cuelga verticalmente hacemos

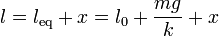
$l = l_\mathrm{eq}+x = l_0+\frac{mg}{k}+x$ $\Rightarrow$ $F = -kx\,$

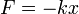
Esto quiere decir que cuando x es positivo, la fuerza es negativa, es decir, tiende a disminuir |x|. Igualmente, si x es negativo, F es positiva, con lo que también tiende a disminuir |x|. El punto de equilibrio es, por tanto, estable.

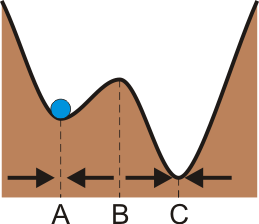
Puede ocurrir que un punto de equilibrio sea estable frente a pequeñas perturbaciones, pero no frente a fuerzas de tamaño finito. Por ejemplo, supongamos una bolita en un perfil como el de la figura. El punto A es de equilibrio estable. Sin embargo una fuerza lo suficientemente intensa puede hacer que la partícula se “entere” de la existencia del mínimo C y caiga en él, pasando por el punto de equilibrio inestable B. Se dice entonces que el punto A es de equilibrio local y C de equilibrio global.

Una de las herramientas más intuitivas para el análisis de la estabilidad es el uso de las curvas de energía potencial, que veremos al analizar la ley de conservación de la energía mecánica.

5 Vínculos. Principio de liberación

5.1 Concepto de vínculo. Clasificación

A menudo una partícula no posee libertad de movimiento en el espacio, sino que se encuentra sometida a vínculos (o ligaduras). Por ejemplo, una partícula suspendida de un péndulo rígido se ve sometida a la restricción $x 2 + y 2 + z 2 = l 2$ . El efecto de un vínculo es la reducción del número de grados de libertad de la partícula, según la ecuación

$r = 3N - k\,$

siendo $r$ el número de grados de libertad, $N$ el número de partículas (en este caso $N = 1$ ) y $k$ el número de vínculos. Para el caso del péndulo, tendremos $r = 2$ . Si además está obligado a moverse sobre un plano vertical, $k = 2$ y $r = 1$ .

Los vínculos pueden clasificarse atendiendo a diferentes criterios.

Unilaterales y bilaterales: Cuando el vínculo impide un desplazamiento en un sentido, pero no en el opuesto, se dice que el vínculo es unilateral. Si impide el movimiento en los dos sentidos, es bilateral. Matemáticamente, un vínculo unilateral se expresa mediante una desigualdad; uno bilateral por una igualdad.

Por ejemplo, un péndulo que cuelga de un hilo flexible supone un vínculo unilateral, expresable como 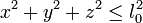$x^2+y^2+z^2\leq l_0^2$ . Si cuelga de una barra rígida es bilateral, cumpliéndose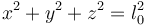 $x^2+y^2+z^2= l_0^2$

Geométricos y cinemáticos: Si un vínculo se puede expresar como una relación sobre las coordenadas de una partícula, se dice que es geométrico. Si además liga a las velocidades, el vínculo es cinemático. Todo vínculo geométrico produce uno cinemático, pero no a la inversa.

Por ejemplo, una partícula obligada a moverse en el extremo de un péndulo rígido está sometida a la condición geométrica

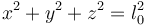
$x^2+y^2+z^2=l_0^2$

Derivando en esta expresión respecto al tiempo llegamos a la condición cinemática

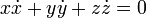
$x\dot{x}+y\dot{y}+z\dot{z}=0$

Una esfera que rueda sobre un plano verifica que la velocidad en el punto de contacto debe ser nula pero de esta condición cinemática no se deduce ningún vínculo geométrico.

Holónomos y no holonómos: Relacionado con lo anterior, un vínculo geométrico o uno cinemático que puede integrarse para dar uno geométrico, se denomina vínculo holónomo. Si es uno cinemático que no conduce a uno geométrico, es no holónomo.

Reónomos y esclerónomos: Si el vínculo es independiente del tiempo se denomina esclerónomo. Si depende del tiempo es reónomo.; Por ejemplo, el vínculo de una partícula en el extremo del péndulo es esclerónomo; una anilla ensartada en una barra horizontal en rotación uniforme está sometida al vínculo reónomo

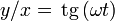
$y/x =\,\mathrm{tg}\,(\omega t)$

5.2 Fuerzas de reacción vincular

La presencia de un vínculo limita los posibles valores de la posición de una partícula. Podemos preguntarnos por el mecanismo físico por el cual el vínculo ejerce su limitación.

Si la posición se ve limitada, también su aceleración se ve afectada. De acuerdo con la segunda ley de Newton, un cambio en la aceleración se debe a la presencia de una fuerza. Por tanto, la presencia de un vínculo se manifiesta como una fuerza adicional ejercida sobre la partícula. Esta fuerza es conocida como fuerza de reacción vincular.

Consideremos el caso de una masa situada sobre una mesa horizontal. En el equilibrio, su aceleración, tanto vertical como horizontal, vertical es nula

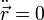
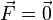
$\ddot{\vec{r}}=0$ $\Rightarrow$ $\vec{F} = \vec{0}\,$

El peso de la partícula está actuando verticalmente sobre ella. Puesto que la fuerza total es nula, concluimos que existe una fuerza vertical, la reacción de la mesa, igual en módulo y de sentido opuesto al peso

$\vec{0} = -mg\vec{k} + \vec{R}\,$ $\Rightarrow$ $\vec{R} = mg\vec{k}$

6 Dinámica de la partícula

6.1 Partícula libre

6.2 Partícula vinculada. principio de liberación

7 Teoremas de conservación

7.1 Integrales primeras

7.2 De la cantidad de movimiento

7.3 Del momento cinético

7.4 De la energía

Dinámica del punto material (G.I.T.I.)

De Laplace

Contenido