Entrar Página Discusión Historial Go to the site toolbox

2.7. Movimiento circular en torno a un eje oblicuo

De Laplace

Contenido

1 Enunciado

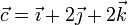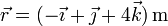Una partícula gira alrededor de un eje que pasa por el origen de coordenadas y está orientado según el vector \vec{c}=\vec{\imath}+2\vec{\jmath}+2\vec{k}. La aceleración angular de este movimiento es constante y de módulo 1 rad/s². La velocidad angular inicial es nula. Si en t = 2\,\mathrm{s} la partícula se encuentra en \vec{r}=(-\vec{\imath}+\vec{\jmath}+4\vec{k})\,\mathrm{m} calcule, para este instante

  1. La velocidad y la aceleración.
  2. Las componentes intrínsecas de la aceleración.

2 Velocidad y aceleración

2.1 Velocidad

La velocidad de una partícula que describe un movimiento circular en torno a un eje puede escribirse en la forma

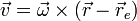
\vec{v}=\vec{\omega}\times(\vec{r}-\vec{r}_e)

siendo 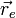\vec{r}_e un punto del eje de giro (no necesariamente el centro de la circunferencia). De acuerdo con el enunciado, podemos tomar este punto como el origen de coordenadas

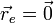
\vec{r}_e = \vec{0}

La velocidad angular la hallamos abiendo que la aceleración angular es constante

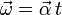
\vec{\omega}=\vec{\alpha}\,t

La aceleración angular es

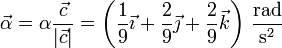
\vec{\alpha}=\alpha\frac{\vec{c}}{|\vec{c}|} = \left(\frac{1}{9}\vec{\imath}+\frac{2}{9}\vec{\jmath}+\frac{2}{9}\vec{k}\right)\,\frac{\mathrm{rad}}{\mathrm{s}^2}

por lo que en t=2\,\mathrm{s} la velocidad angular vale

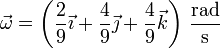
\vec{\omega}=\left(\frac{2}{9}\vec{\imath}+\frac{4}{9}\vec{\jmath}+\frac{4}{9}\vec{k}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}

Multiplicando vectorialmente por el vector de posición

3 Componentes de la aceleración

Obtenido de "http://tesla.us.es/wiki/index.php/2.7._Movimiento_circular_en_torno_a_un_eje_oblicuo"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace