Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Sistema de ecuaciones vectoriales

De Laplace

Revisión a fecha de 21:54 14 sep 2010; Antonio (Discusión | contribuciones)
(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado

Demuestre que si se cumplen simultáneamente las condiciones

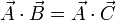
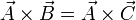
\vec{A}\cdot\vec{B} = \vec{A}\cdot\vec{C}        \vec{A}\times\vec{B} = \vec{A}\times\vec{C}

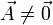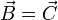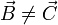siendo \vec{A}\neq \vec{0}, entonces \vec{B} = \vec{C}; pero si se cumple una de ellas y la otra no, entonces \vec{B}\neq\vec{C}.

2 Introducción

Existen varias formas de abordar este problema:

  • Empleando las propiedades cancelativas.
  • Mediante argumentos geométricos.
  • Empleando el doble producto vectorial.

Veremos cada uno de estos tres métodos por separado.

3 Propiedades cancelativas

4 Solución geométrica

5 Doble producto vectorial

Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Sistema_de_ecuaciones_vectoriales"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace