Campo magnético de una esfera rotatoria
De Laplace
Contenido |
1 Enunciado
Una esfera de radio a almacena una carga Q distribuida uniformemente en su superficie. La esfera gira con velocidad angular ω alrededor de un eje.
-
 Determine la densidad de corriente en la esfera
Determine la densidad de corriente en la esfera
-
 Calcule, por integración directa, el campo magnético en los puntos del eje de rotación.
Calcule, por integración directa, el campo magnético en los puntos del eje de rotación.
-
 Calcule el momento dipolar magnético de la esfera. A partir de aquí, halle el campo en puntos alejados de la esfera, no necesariamente en el eje.
Calcule el momento dipolar magnético de la esfera. A partir de aquí, halle el campo en puntos alejados de la esfera, no necesariamente en el eje.
-
 Halle, resolviendo las ecuaciones de la magnetostática, el campo en todos los puntos del espacio.
Halle, resolviendo las ecuaciones de la magnetostática, el campo en todos los puntos del espacio.
2 Densidad de corriente
Puesto que la densidad de carga se encuentra sobre la superficie de la esfera, la densidad de corriente resultante va a ser una superficial, 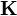 . Si tenemos una distribución de carga superficial fijada en un sólido, el cual se mueve con velocidad
. Si tenemos una distribución de carga superficial fijada en un sólido, el cual se mueve con velocidad  , la densidad de corriente será
, la densidad de corriente será
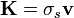
puesto que todos los portadores de carga de un elemento de superficie se mueven con la misma velocidad.
Para el caso de distribución uniforme
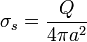
y un movimiento de rotación, empleando coordenadas esféricas
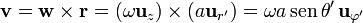
y esto nos da la densidad de corriente
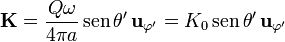
3 Campo en el eje
Podemos calcular el campo integrando desde el principio, con ayuda de la ley de Biot y Savart
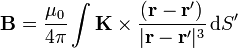
No, obstante, para evitar cálculos repetitivos, podemos hacer uso de resultados conocidos. Si cortamos la esfera mediante planos perpendiculares al eje de giro, la reducimos a un conjunto de espiras circulares, cada una de las cuales produce un campo conocido. Superponiendo el campo de las espiras diferenciales obtendremos el campo de la esfera completa.
El campo de una espira circular situada en el plano z' = 0 es
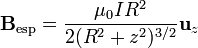
Si no se encuentra en el plano coordenado sino a una altura z' se traslada esta coordenada
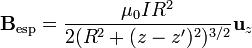
En nuestro caso, el radio de la espira también depende de la altura a la que se encuentra. De acuerdo con el teorema de Pitágoras
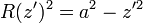

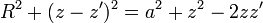
La intensidad de corriente para cada espira diferencial es la carga que pasa por un punto de ella en intervalo de tiempo dado
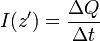
En un intervalo igual al periodo de revolución
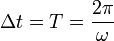
la cantidad de carga que pasa es la contenida en un anillo de radio 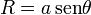 y espesor
y espesor 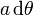

Teniendo en cuenta que z' = acosθ esta carga equivale a
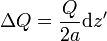

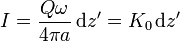
El resultado es que por todas las espiras circula la misma corriente diferencial.
Sumando todas las contribuciones, el campo en los puntos del eje es
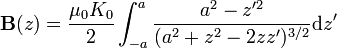
Esta integral se resuleve con el cambio de variable
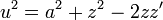
Esta cantidad u representa la distancia del punto de observación a una de las espiras. Sus valores extremos son (recordando que la raíz cuadrada es siempre positiva)
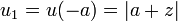
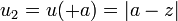
Este cambio de variable convierte la integral en suma de tres integrales de potencias elementales. El resultado general se puede simplificar distinguiendo si el punto de observación se encuentra dentro de la esfera ( − a < z < a) o fuera de ella ( | z | > a). El resultado es
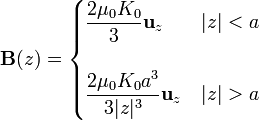
Este campo es constante dentro de la esfera, y puramente dipolar (decae como z3) fuera de ella.
4 Momento dipolar
4.1 A partir de la corriente
El momento dipolar magnético para una distribución de corriente superficial es
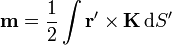
Empleando coordenadas esféricas, cada uno de los términos de esta integral valen
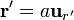
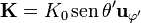
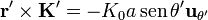
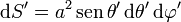
Puesto que se trata de una integral vectorial, hay que pasar a la base cartesiana, ya que, en esféricas,
Aplicamos que
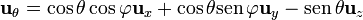
y la integral se puede descomponer en esta base
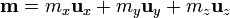
con
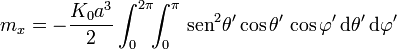
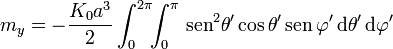
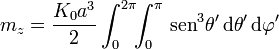
las dos primeras integrales se anulan ya que
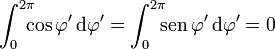
La tercera componente se convierte en un producto de dos integrales independientes
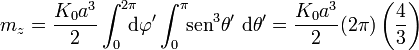
Simplificando nos queda el momento dipolar magnético
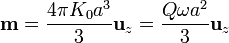
4.2 A partir del campo magnético
El momento dipolar puede deducirse del campo magnético en los puntos del eje. La expresión general del campo magnético de un dipolo es
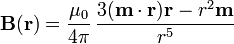
En los puntos del eje Z posiitivo, este campo se reduce a
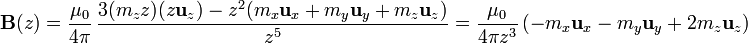
Comparando este resultado con el de la sección anterior obtenemos, igualando componente a componente,
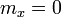
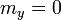
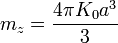

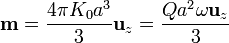
4.3 Campo lejos de la esfera
Una vez que tenemos el momento dipolar, podemos hallar el campo aproximado en todos los puntos exteriores alejados de la esfera, no necesariamente sobre el eje:
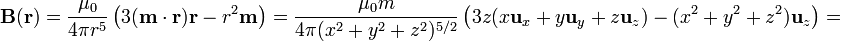
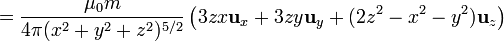
o, en coordenadas esféricas
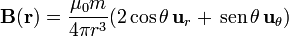
5 Campo en todo el espacio
5.1 Planteamiento
Veamos cómo se determina el campo magnético de forma exacta en todos los puntos del espacio, resolviendo las ecuaciones de la magnetostática.
Este sistema posee simetría acimutal, por lo que ninguna de las componentes de los vectores depende de la coordenada  .
.
Además, las corrientes van únicamente en la dirección de  . Esto nos permite suponer un potencial vector
. Esto nos permite suponer un potencial vector
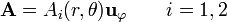
donde el subíndice i indica si estamos dentro (1) de la esfera o fuera (2) de ella.
Esta suposición puede no resultar evidente, pero en última instancia estamos protegidos por el teorema de existencia y unicidad. Si la solución que encontramos cumple todas las ecuaciones y condiciones de contorno,será la solución del problema.
El campo magnético lo obtenemos hallando el rotacional del potencial vector. Resultan las componentes
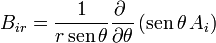
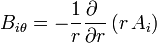
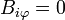
Sustituyendo ahora en las ecuaciones de la magnetostática, tenemos que  cumple automáticamente la ley de Gauss para el campo magnético por ser un rotacional. En cuanto a la ley de Ampère tenemos que, por ser nula la densidad de corriente de volumen
cumple automáticamente la ley de Gauss para el campo magnético por ser un rotacional. En cuanto a la ley de Ampère tenemos que, por ser nula la densidad de corriente de volumen
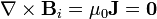
tanto dentro como fuera de la esfera. Hallando el rotacional del campo magnético y sustituyendo las expresiones anteriores nos queda la ecuación diferencial
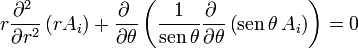
Ésta no es la ecuación de Laplace, aunque se le parece.
En cuanto a las condiciones de contorno en la superficie de la esfera (r = a) se cumple que la componente normal (en este caso, la radial) del campo magnético es continua
![\mathbf{n}\cdot[\mathbf{B}]=0](/wiki/images/math/c/8/2/c82827f0b3e04bed75d70b5a389b9608.png)

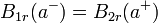

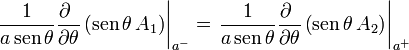
De la ley de Ampère obtenemos que el salto en la componente tangencial es proporcional a la densidad de corriente superficial
![\mathbf{n}\times[\mathbf{B}]=\mu_0\mathbf{K}\,](/wiki/images/math/a/7/0/a70b6537202ac1f836c05cd7fe7f71b5.png)

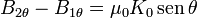

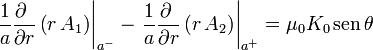
A estas condiciones debemos añadir que el potencial vector debe anularse lejos de la esfera
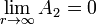
y que no debe ser singular en el centro de la esfera, ya que no hay corrientes en dicho punto
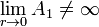
5.2 Potencial vector
En lugar de atacar el problema como uno en dos variables (r y θ), haremos una hipótesis adicional sobre la solución. Puesto que las únicas fuentes del campo magnético son las corrientes superficiales y estas dependen del ángulo θ como el seno, vamos a suponer la forma del potencial vector
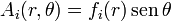
con lo que reducimos el problema a hallar la dependencia radial (de nuevo, nos apoyamos en el teorema de existencia y unicidad). Sustituyendo en la ecuación de volumen obtenemos la ecuación diferencial

o, desarrollando la derivada,
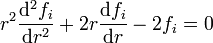
Las condiciones de contorno en la superficie de la esfera se convierten en
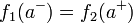
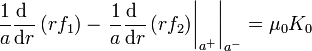
La ecuación diferencial es equidimensional, o de Euler, por lo que tiene por soluciones potencias. Sustituyendo y hallando los exponentes llegamos finalmente a la solución
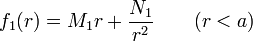
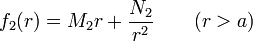
Ahora bien, el campo no puede tener a infinito ni en el origen ni en el infinito, por lo que
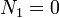
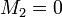
Las condiciones de salto en la superficie nos dan las ecuaciones para los coeficientes
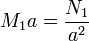
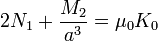
con solución
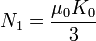
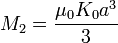
Sustituyendo llegamos por fin a la expresión del potencial vector en todo el espacio
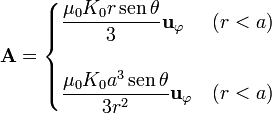
Este potencial vector cumple la ecuación diferencial y todas las condiciones de salto y de contorno; por tanto, es la solución del problema.
5.3 Campo magnético
5.3.1 En el interior de la esfera
Las componentes, en esféricas, del campo magnético interior son
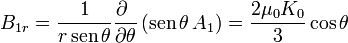

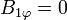
En forma vectorial
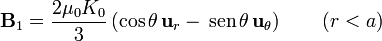
Aplicando las relaciones entre las bases, llegamos al sencillo resultado, en cartesianas
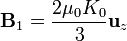
esto es, el campo magnético en el interior de la esfera es uniforme. Tiene el mismo valor en todos los puntos del interior, no solo los del eje.
5.3.2 En el exterior de la esfera
Hallando, del mismo modo, el campo en el exterior de la esfera, llegamos a
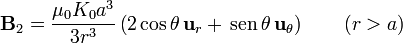
Este es el campo de un dipolo magnético. Por ello, la esfera se ve como un dipolo no solo en los puntos alejados, y no solo en los puntos del eje, sino en todo el espacio exterior a la esfera. El desarrollo multipolar da en este caso un resultado exacto.
El momento dipolar correspondiente, a partir de esta expresión, es
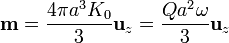
5.4 Líneas de campo magnético
Las líneas de campo magnético en este sistema se componen de dos tramos:
- Uno rectilíneo, hacia arriba, por el interior de la esfera, donde el campo es uniforme.
- Uno en forma de lóbulo, hacia abajo, por el exterior, donde el campo es dipolar.
El resultado son líneas de campo cerradas (lo que es de esperar en un campo solenoidal) que dan vueltas en torno a la corriente superficial, según la regla de la mano derecha.







