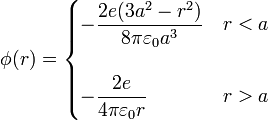Entrar Página Discusión Historial Go to the site toolbox

Modelo de molécula de hidrógeno

De Laplace

Contenido

1 Enunciado

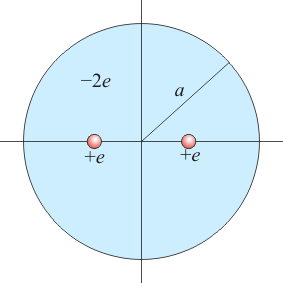
Un modelo simple de la molécula de hidrógeno es el siguiente: tenemos dos cargas puntuales (los núcleos) de valor + e inmersas en una nube esférica de radio a, con carga − 2e distribuida uniformemente.

  1. Determine la posición de equilibrio entre las dos cargas puntuales, suponiendo que se encuentran situadas simétricamente respecto al centro de la nube.
  2. Calcule el potencial y el campo eléctrico en todos los puntos del espacio en la situación anterior.
  3. Suponga que las dos cargas positivas se desplazan una cantidad c = a / 4 a lo largo de la recta que las une, manteniendo la distancia entre ellas. En este caso, ¿qué campo se ve en el exterior de la molécula? ¿cuáles son los dos primeros momentos del desarrollo multipolar del potencial eléctrico?
  4. Calcule el trabajo necesario para realizar el desplazamiento del apartado anterior.

2 Posición de equilibrio

Las cargas positivas se repelen mutuamente. Sin embargo no se alejan indefinidamente debido a la fuerza debida a la nube negativa, que las empuja hacia el centro y que es más intensa cuanto más se alejan del centro.

La condición de equilibrio para una de las cargas positivas es que la fuerza total sobre ella se anule

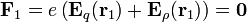
\mathbf{F}_1=e\left(\mathbf{E}_q(\mathbf{r}_1)+\mathbf{E}_\rho(\mathbf{r}_1)\right)=\mathbf{0}

Si suponemos uno de los núcleos, de carga + e situado en 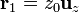\mathbf{r}_1=z_0\mathbf{u}_z y el otro en 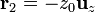\mathbf{r}_2=-z_0\mathbf{u}_z, el campo que el segundo produce en la posición del primero es

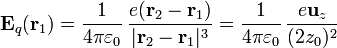
\mathbf{E}_q(\mathbf{r}_1)=\frac{1}{4\pi\varepsilon_0}\,\frac{e(\mathbf{r}_2-\mathbf{r}_1)}{|\mathbf{r}_2-\mathbf{r}_1|^3}=\frac{1}{4\pi\varepsilon_0}\,\frac{e\mathbf{u}_z}{(2z_0)^2}

El campo debido a la nube de carga puede calcularse aplicando la ley de Gauss y el resultado es

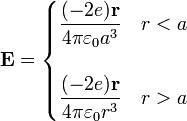
\mathbf{E}=\begin{cases}\displaystyle\frac{(-2e)\mathbf{r}}{4\pi\varepsilon_0 a^3} & r < a \\ & \\ \displaystyle\frac{(-2e)\mathbf{r}}{4\pi\varepsilon_0 r^3} & r > a\end{cases}

En la posición ocupada por el primer núcleo, este campo vale

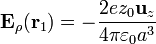
\mathbf{E}_\rho(\mathbf{r}_1) = -\frac{2ez_0\mathbf{u}_z}{4\pi\varepsilon_0a^3}

La condición de equilibrio es entonces

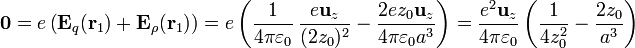
\mathbf{0}=e\left(\mathbf{E}_q(\mathbf{r}_1)+\mathbf{E}_\rho(\mathbf{r}_1)\right)=e\left(\frac{1}{4\pi\varepsilon_0}\,\frac{e\mathbf{u}_z}{(2z_0)^2}-\frac{2ez_0\mathbf{u}_z}{4\pi\varepsilon_0a^3}\right) = \frac{e^2\mathbf{u}_z}{4\pi\varepsilon_0}\left(\frac{1}{4z_0^2}-\frac{2z_0}{a^3}\right)

que tiene por solución

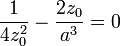
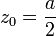
\frac{1}{4z_0^2}-\frac{2z_0}{a^3} = 0   \Rightarrow    z_0 = \frac{a}{2}

Por tanto, la molécula está formada por dos núcleos situados simétricamente a ambos lados del centro de la nube, a una distancia del centro igual a la mitad del radio de la nube.

3 Potencial y campo eléctrico

3.1 Campo eléctrico

El campo eléctrico en cualquier punto del espacio será la suma del de las dos cargas puntuales, más el de la nube de carga, que hemos enunciado más arriba. Si distinguimos entre el interior y el exterior de ésta tenemos:

Exterior de la molécula
Desde fuerza de la molécula, las dos cargas puntuales se ven como tales, mientras que la nube de carga se ve como una tercera carga puntual situada en el centro de la nube, y de magnitud − 2e. El campo total es entonces
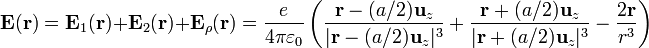
\mathbf{E}(\mathbf{r})=\mathbf{E}_1(\mathbf{r})+\mathbf{E}_2(\mathbf{r})+\mathbf{E}_\rho(\mathbf{r})=\frac{e}{4\pi\varepsilon_0} \left(\frac{\mathbf{r}-(a/2)\mathbf{u}_z}{|\mathbf{r}-(a/2)\mathbf{u}_z|^3}+\frac{\mathbf{r}+(a/2)\mathbf{u}_z}{|\mathbf{r}+(a/2)\mathbf{u}_z|^3}-\frac{2\mathbf{r}}{r^3}\right)
Nótese que aunque la molécula es neutra (la nube tiene la misma carga que los dos núcleos juntos y con signo opuesto) el campo exterior no es nulo.
Interior de la molécula
Dentro de la molécula, las dos cargas puntuales se siguen viendo como puntuales, mientras que la nube de carga produce un campo que varía linealmente con la distancia. El campo total es entonces
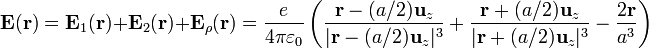
\mathbf{E}(\mathbf{r})=\mathbf{E}_1(\mathbf{r})+\mathbf{E}_2(\mathbf{r})+\mathbf{E}_\rho(\mathbf{r})=\frac{e}{4\pi\varepsilon_0} \left(\frac{\mathbf{r}-(a/2)\mathbf{u}_z}{|\mathbf{r}-(a/2)\mathbf{u}_z|^3}+\frac{\mathbf{r}+(a/2)\mathbf{u}_z}{|\mathbf{r}+(a/2)\mathbf{u}_z|^3}-\frac{2\mathbf{r}}{a^3}\right)

3.2 Potencial eléctrico

Para el potencial eléctrico aplicamos de nuevo el principio de superposición. El potencial total será el de las dos cargas más el de la nube. El potencial de cada carga puntual es

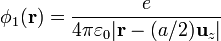
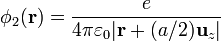
\phi_1(\mathbf{r})=\frac{e}{4\pi\varepsilon_0|\mathbf{r}-(a/2)\mathbf{u}_z|}        \phi_2(\mathbf{r})=\frac{e}{4\pi\varepsilon_0|\mathbf{r}+(a/2)\mathbf{u}_z|}

Para el potencial debido a la nube integramos el campo desde el infinito hasta una cierta distancia del centro.

Exterior de la esfera
El campo es en todos los puntos el de una carga puntual, por lo que el potencial también lo es
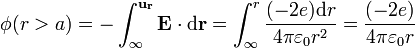
\phi(r>a) = -\int_{\infty}^\mathbf{\mathbf{u}_r}\mathbf{E}\cdot\mathrm{d}\mathbf{r}= \int_\infty^r \frac{(-2e)\mathrm{d}r}{4\pi\varepsilon_0 r^2} = \frac{(-2e)}{4\pi \varepsilon_0 r}
Interior de la esfera
Para llegar al interior, la integral se compone de dos tramos, uno desde el infinito hasta el borde de la nube, y otro desde ahí hasta el punto donde queremos hallar el potencial
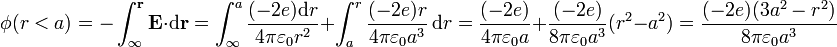
\phi(r<a) = -\int_{\infty}^\mathbf{\mathbf{r}}\mathbf{E}\cdot\mathrm{d}\mathbf{r}= \int_\infty^a \frac{(-2e)\mathrm{d}r}{4\pi\varepsilon_0 r^2}+\int_a^r \frac{(-2e)r}{4\pi\varepsilon_0 a^3}\,\mathrm{d}r = \frac{(-2e)}{4\pi \varepsilon_0 a}+\frac{(-2e)}{8\pi \varepsilon_0 a^3}(r^2-a^2)=\frac{(-2e)(3a^2-r^2)}{8\pi\varepsilon_0 a^3}

Combinando ambos resultados:

\phi(r)=\begin{cases}\displaystyle -\frac{2e(3a^2-r^2)}{8\pi\varepsilon_0 a^3} & r < a \\ & \\ \displaystyle -\frac{2e}{4\pi\varepsilon_0 r} & r > a\end{cases}

4 Desarrollo multipolar

4.1 Campo exterior

4.2 Primeros momentos

5 Trabajo eléctrico

Obtenido de "http://tesla.us.es/wiki/index.php/Modelo_de_mol%C3%A9cula_de_hidr%C3%B3geno"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace