Enunciado de Kelvin-Planck
De Laplace
Contenido |
1 Introducción
Cuando se estudian las máquinas térmicas se obtiene que el rendimiento de estas máquinas viene dado por
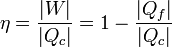
siendo | W | el trabajo neto realizado por la máquina, | Qc | el calor que absorbe del foco caliente para realizar dicho trabajo y | Qf | el calor de desecho que es entregado al foco frío (normalmente el ambiente).
A la hora de aumentar la eficiencia de una máquina, el primer objetivo sería reducir, o eliminar si es posible, ese calor de desecho. Se plantean dos alternativas
- ¿Es posible una máquina térmica que no genere calor de desecho, sino que todo el calor absorbido se transforme en trabajo neto?
- ¿Es posible una reutilización del calor de desecho, de forma que se haga recircular y se incluya en el calor absorbido?
La respuesta a ambas preguntas es negativa.
2 Enunciado
El enunciado de Kelvin-Planck del segundo principio de la termodinámica es el siguiente:
Es imposible construir una máquina que, operando en un ciclo, produzca como único efecto la extracción de calor de un foco y la realización de una cantidad equivalente de trabajo
Este enunciado afirma la imposibilidad de construir una máquina que convierta todo el calor en trabajo. Siempre es necesario intercambiar calor con un segundo foco (el foco frío), de forma que parte del calor absorbido se expulsa como calor de desecho al ambiente.
Matemáticamente, esto implica que el rendimiento de una máquina térmica, que según el Primer Principio de la Termodinámica podría ser igual a la unidad, es en realidad siempre menor que la unidad
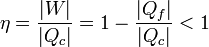
De la equivalencia con el teorema de Carnot que aparece más adelante se deduce que, de hecho, es un número habitualmente mucho menor que la unidad.
El enunciado de Kelvin-Planck está enunciado de manera negativa: nos dice lo que no es posible, no lo que es posible. Se expone además sin justificación previa: simplemente refleja un hecho empírico, que no ha sido refutado por ninguna experiencia. Es posible, no obstante, justificar el segundo principio de la termodinámica acudiendo a la visión microscópica de los sistemas.





