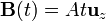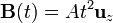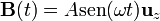Espira circular en un campo variable
De Laplace
Revisión a fecha de 17:58 24 may 2008; Gonfer (Discusión | contribuciones)
Contenido |
1 Enunciado
Una espira circular de radio  , con autoinducción
, con autoinducción  y resistencia
y resistencia  , se encuentra sometida a un campo magnético uniforme en el espacio pero variable en el tiempo. El campo es perpendicular al plano de la espira.
, se encuentra sometida a un campo magnético uniforme en el espacio pero variable en el tiempo. El campo es perpendicular al plano de la espira.
Calcule la corriente que circula por la espira si el campo magnético varía en el tiempo, durante un largo intervalo, como