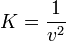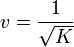Pulso en una cuerda
De Laplace
Revisión a fecha de 20:15 26 mar 2010; Gonfer (Discusión | contribuciones)
1 Enunciado
Los puntos de una cuerda horizontal se mueven verticalmente, de forma que el perfil de la cuerda tiene la forma
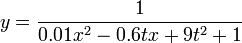
donde x e y se miden en centímetros y t en segundos.
- Halle la velocidad de esta onda.
- Demuestre que esta señal cumple la ecuación de onda.
- Calcule la velocidad del punto de la cuerda situado en x = 15 cm, en (a) t = 0 s, (b) t = 0.5 s, (c) t = 1 s.
2 Solución
Podemos resolver los dos primeros apartados simultáneamente. Si calculamos la segunda derivada respecto a x la segunda derivada respecto a t y obtenemos que ambas son proporcionales
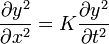
entonces podemos afirmar que verifica la ecuación de onda y además que