Fuerza de Lorentz sobre una esfera en rotación

De Laplace

Revisión a fecha de 20:16 15 mar 2010; Gonfer (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Fuerza sobre la distribución
3 Momento sobre la distribución
- 3.1 Torque eléctrico
- 3.2 Torque magnético

1 Introducción

Suponemos una distribución de carga que posee simetría esférica alrededor de un punto central 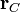$\mathbf{r}_C$ , de forma que su densidad de carga verifica

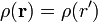
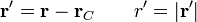
$\rho(\mathbf{r})=\rho(r')\,$ $\mathbf{r}'=\mathbf{r}-\mathbf{r}_C\qquad r'=|\mathbf{r}'|$

Suponemos que esta distribución de carga está localizada, de forma que tiende a cero rápidamente cuando $r'$ crece

Esta distribución de carga se mueve rígidamente, de forma que la velocidad de cada punto puede escribirse como

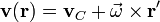
$\mathbf{v}(\mathbf{r})=\mathbf{v}_C+\vec{\omega}\times\mathbf{r}'$

Asimismo, esta distribución se encuentra en el seno de un campo electromagnético externo, de forma que cada elemento de carga se encuentra sometido a una fuerza

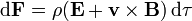
$\mathrm{d}\mathbf{F}=\rho(\mathbf{E}+\mathbf{v}\times\mathbf{B})\,\mathrm{d}\tau$

2 Fuerza sobre la distribución

La fuerza neta sobre la distribución de carga será la resultante de las fuerzas diferenciales

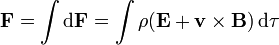
$\mathbf{F}=\int \mathrm{d}\mathbf{F}=\int\rho(\mathbf{E}+\mathbf{v}\times\mathbf{B})\,\mathrm{d}\tau$

Veamos cada contribución por separado.

2.1 Fuerza eléctrica

La fuerza eléctrica sobre la distribución será

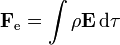
$\mathbf{F}_\mathrm{e}=\int \rho\mathbf{E}\,\mathrm{d}\tau$

Podemos calcular una expresión aproximada para esta fuerza aplicando que la distribución de carga está localizada en torno a su centro, de manera que podemos sustituir el campo eléctrico por su desarrollo en serie de Taylor en torno al centro de la distribución

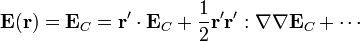
$\mathbf{E}(\mathbf{r})=\mathbf{E}_C = \mathbf{r}'\cdot\mathbf{E}_C+\frac{1}{2}\mathbf{r}'\mathbf{r}':\nabla\nabla\mathbf{E}_C + \cdots$

donde 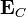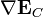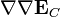$\mathbf{E}_C$ , $\nabla\mathbf{E}_C$ , $\nabla\nabla\mathbf{E}_C$ son constantes iguales al valor del campo y sus derivadas sucesivas en el centro de la distribución.

De esta forma la fuerza eléctrica viene dada por la serie

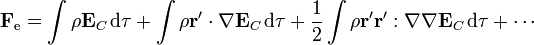
$\mathbf{F}_\mathrm{e}= \int \rho \mathbf{E}_C\,\mathrm{d}\tau+ \int \rho \mathbf{r}'\cdot\nabla\mathbf{E}_C\,\mathrm{d}\tau + \frac{1}{2}\int \rho \mathbf{r}'\mathbf{r}':\nabla\nabla\mathbf{E}_C\,\mathrm{d}\tau+\cdots$

y, sacando las constantes fuera de las integrales

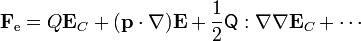
$\mathbf{F}_\mathrm{e}=Q\mathbf{E}_C+(\mathbf{p}\cdot\nabla)\mathbf{E}+\frac{1}{2}\mathsf{Q}:\nabla\nabla\mathbf{E}_C+\cdots$

donde

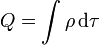
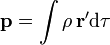
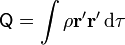
$Q=\int\rho\,\mathrm{d}\tau$ $\mathbf{p}=\int\rho\,\mathbf{r}'\mathrm{d}\tau$ $\mathsf{Q}=\int \rho\mathbf{r}'\mathbf{r}'\,\mathrm{d}\tau$

Aquí $Q$ es la carga neta de la distribución. 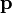$\mathbf{p}$ es el momento dipolar, el cual se anula debido a la simetría de la distribución.

El término 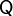$\mathsf{Q}$ es un tensor. Por la simetría de la distribución, este tensor es realmente un escalar, ya que

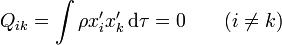
$Q_{ik}=\int \rho x'_ix'_k\,\mathrm{d}\tau=0\qquad(i\neq k)$

y

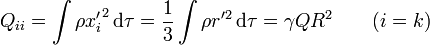
$Q_{ii}=\int \rho {x'_i}^2\,\mathrm{d}\tau = \frac{1}{3}\int \rho r'^2 \,\mathrm{d}\tau = \gamma QR^2 \qquad (i=k)$

aquí $γ$ es un coeficiente que depende de la forma concreta de la distribución. Para una esfera cargada uniformemente en volumen vale 1/5, para una cargada en superficie es 1/3, para un decaimiento exponencial vale 4. Reuniendo los dos resultados

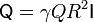
$\mathsf{Q}=\gamma Q R^2 \mathsf{I}\,$

Llevando esto a la expresión de la fuerza, queda

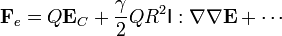
$\mathbf{F}_e = Q\mathbf{E}_C + \frac{\gamma}{2}QR^2\mathsf{I}:\nabla\nabla\mathbf{E}+\cdots$

pero la contracción del tensor unidad con el gradiente del gradiente es simplemente el laplaciano

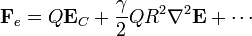
$\mathbf{F}_e = Q\mathbf{E}_C + \frac{\gamma}{2}QR^2\nabla^2\mathbf{E}+\cdots$

Ahora, para un campo eléctrico externo estático y debido a cargas en posiciones no coincidentes con la distribución (como es el caso del campo de un núcleo sobre un electrón), el laplaciano del campo eléctrico se anula y la fuerza se reduce a

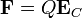
$\mathbf{F}=Q\mathbf{E}_C$

Hay que señalar que el término en $Q R 2$ no es un término cuadrupolar. El término cuadrupolar se refiere a la componente simétrica de traza nula. El término que sale aquí se debe a que el centro de fuerzas eléctricas no coincide con el centro de la distribución.

2.2 Fuerza magnética

La fuerza magnética sobre la distribución será

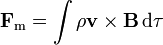
$\mathbf{F}_\mathrm{m}=\int \rho\mathbf{v}\times\mathbf{B}\,\mathrm{d}\tau$

Sustituyendo la expresión de la velocidad

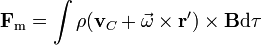
$\mathbf{F}_\mathrm{m}=\int\rho(\mathbf{v}_C+\vec{\omega}\times\mathbf{r}')\times\mathbf{B}\mathrm{d}\tau$

Para el primer término tenemos

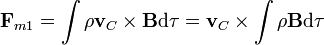
$\mathbf{F}_{m1}=\int \rho\mathbf{v}_C\times\mathbf{B}\mathrm{d}\tau = \mathbf{v}_C\times\int\rho \mathbf{B}\mathrm{d}\tau$

Aquí podemos hacer el mismo desarrollo que para el campo eléctrico y nos queda

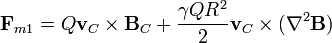
$\mathbf{F}_{m1}=Q\mathbf{v}_C\times\mathbf{B}_C + \frac{\gamma QR^2}{2}\mathbf{v}_C\times(\nabla^2\mathbf{B})$

De nuevo, si este campo magnético se debe a fuentes situadas fuera de la distribución (como el núcleo sobre un electrón), el laplaciano del campo magnético es nulo y este término se reduce a

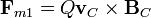
$\mathbf{F}_{m1}=Q\mathbf{v}_C\times\mathbf{B}_C$

Para el segundo término desarrollamos el doble producto vectorial

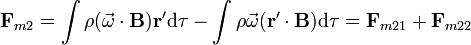
$\mathbf{F}_{m2}=\int \rho (\vec{\omega}\cdot\mathbf{B})\mathbf{r}'\mathrm{d}\tau-\int \rho \vec{\omega}(\mathbf{r}'\cdot\mathbf{B})\mathrm{d}\tau=\mathbf{F}_{m21}+\mathbf{F}_{m22}$

Aplicando ahora la serie de Taylor para el campo magnético

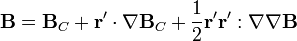
$\mathbf{B}=\mathbf{B}_C+\mathbf{r}'\cdot\nabla\mathbf{B}_C+\frac{1}{2}\mathbf{r}'\mathbf{r}':\nabla\nabla\mathbf{B}$

obtenemos en primer lugar

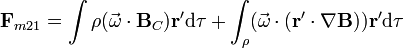
$\mathbf{F}_{m21}=\int \rho (\vec{\omega}\cdot\mathbf{B}_C)\mathbf{r}'\mathrm{d}\tau+\int_\rho(\vec{\omega}\cdot(\mathbf{r}'\cdot\nabla\mathbf{B}))\mathbf{r}'\mathrm{d}\tau$

En primer término es nulo, por la simetría. Para el segundo, empleando subíndices

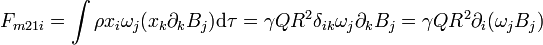
$F_{m21i}=\int \rho x_i\omega_j(x_k\partial_k B_j)\mathrm{d}\tau = \gamma QR^2 \delta_{ik} \omega_j\partial_k B_j = \gamma QR^2 \partial_i(\omega_jB_j)\,$

o, en forma vectorial

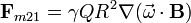
$\mathbf{F}_{m21} = \gamma QR^2 \nabla(\vec{\omega}\cdot\mathbf{B})$

Para 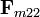$\mathbf{F}_{m22}$ tenemos, igualmente

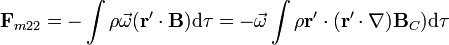
$\mathbf{F}_{m22}=-\int \rho \vec{\omega}(\mathbf{r}'\cdot\mathbf{B})\mathrm{d}\tau =-\vec{\omega}\int \rho\mathbf{r}'\cdot(\mathbf{r}'\cdot\nabla)\mathbf{B}_C)\mathrm{d}\tau$

Empleando de nuevo subíndices

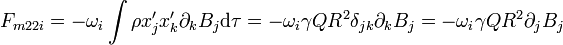
$F_{m22i} = -\omega_i \int \rho x'_jx'_k\partial_k B_j\mathrm{d}\tau = -\omega_i \gamma QR^2 \delta_{jk}\partial_kB_j=-\omega_i \gamma QR^2 \partial_jB_j\,$

En forma vectorial

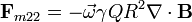
$\mathbf{F}_{m22}=-\vec{\omega}\gamma QR^2 \nabla\cdot\mathbf{B}$

pero la divergencia del campo magnético es siempre nula, por lo que este término se anula. Nos queda por tanto la fuerza magnética

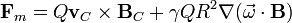
$\mathbf{F}_m = Q\mathbf{v}_C\times\mathbf{B}_C+ \gamma QR^2\nabla(\vec{\omega}\cdot\mathbf{B})$

2.3 Fuerza total

Sumando las fuerzas eléctrica y magnética obtenemos la fuerza neta

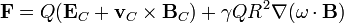
$\mathbf{F}=Q(\mathbf{E}_C+\mathbf{v}_C\times\mathbf{B}_C)+\gamma QR^2 \nabla(\omega\cdot\mathbf{B})$

Si las fuentes del campo eléctrico y magnético coinciden con lso puntos de la distribución, habrá que añadir los términos correspondientes a los laplacianos de los campos.

3 Momento sobre la distribución

De manera análoga se halla el momento de las fuerzas respecto al centro de la distribución. Este momento será

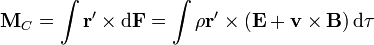
$\mathbf{M}_C=\int \mathbf{r}'\times\mathrm{d}\mathbf{F}=\int\rho\mathbf{r}'\times(\mathbf{E}+\mathbf{v}\times\mathbf{B})\,\mathrm{d}\tau$

Como con la fuerza, consideraremos cada momento por separado.

Fuerza de Lorentz sobre una esfera en rotación

De Laplace

Contenido

1 Introducción

2 Fuerza sobre la distribución

2.1 Fuerza eléctrica

2.2 Fuerza magnética

2.3 Fuerza total

3 Momento sobre la distribución

3.1 Torque eléctrico

3.2 Torque magnético

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES