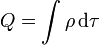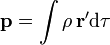Fuerza de Lorentz sobre una esfera en rotación

De Laplace

Revisión a fecha de 16:20 15 mar 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Fuerza sobre la distribución
3 Momento sobre la distribución
- 3.1 Torque eléctrico
- 3.2 Torque magnético

1 Introducción

Suponemos una distribución de carga que posee simetría esférica alrededor de un punto central 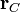$\mathbf{r}_C$ , de forma que su densidad de carga verifica

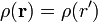
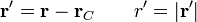
$\rho(\mathbf{r})=\rho(r')\,$ $\mathbf{r}'=\mathbf{r}-\mathbf{r}_C\qquad r'=|\mathbf{r}'|$

Suponemos que esta distribución de carga está localizada, de forma que tiende a cero rápidamente cuando $r'$ crece

Esta distribución de carga se mueve rígidamente, de forma que la velocidad de cada punto puede escribirse como

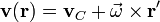
$\mathbf{v}(\mathbf{r})=\mathbf{v}_C+\vec{\omega}\times\mathbf{r}'$

Asimismo, esta distribución se encuentra en el seno de un campo electromagnético externo, de forma que cada elemento de carga se encuentra sometido a una fuerza

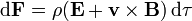
$\mathrm{d}\mathbf{F}=\rho(\mathbf{E}+\mathbf{v}\times\mathbf{B})\,\mathrm{d}\tau$

2 Fuerza sobre la distribución

La fuerza neta sobre la distribución de carga será la resultante de las fuerzas diferenciales

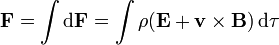
$\mathbf{F}=\int \mathrm{d}\mathbf{F}=\int\rho(\mathbf{E}+\mathbf{v}\times\mathbf{B})\,\mathrm{d}\tau$

Veamos cada contribución por separado.

2.1 Fuerza eléctrica

La fuerza eléctrica sobre la distribución será

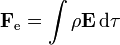
$\mathbf{F}_\mathrm{e}=\int \rho\mathbf{E}\,\mathrm{d}\tau$

Podemos calcular una expresión aproximada para esta fuerza aplicando que la distribución de carga está localizada en torno a su centro, de manera que podemos sustituir el campo eléctrico por su desarrollo en serie de Taylor en torno al centro de la distribución

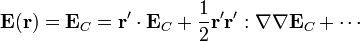
$\mathbf{E}(\mathbf{r})=\mathbf{E}_C = \mathbf{r}'\cdot\mathbf{E}_C+\frac{1}{2}\mathbf{r}'\mathbf{r}':\nabla\nabla\mathbf{E}_C + \cdots$

donde 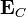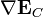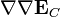$\mathbf{E}_C$ , $\nabla\mathbf{E}_C$ , $\nabla\nabla\mathbf{E}_C$ son constantes iguales al valor del campo y sus derivadas sucesivas en el centro de la distribución.

De esta forma la fuerza eléctrica viene dada por la serie

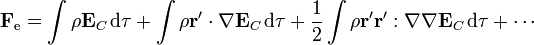
$\mathbf{F}_\mathrm{e}= \int \rho \mathbf{E}_C\,\mathrm{d}\tau+ \int \rho \mathbf{r}'\cdot\nabla\mathbf{E}_C\,\mathrm{d}\tau + \frac{1}{2}\int \rho \mathbf{r}'\mathbf{r}':\nabla\nabla\mathbf{E}_C\,\mathrm{d}\tau+\cdots$

y, sacando las constantes fuera de las integrales