Teorema de conservación de la energía mecánica
De Laplace
Contenido |
1 Teorema de las fuerzas vivas
El trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C es igual a la suma de los trabajos elementales a lo largo de dicha curva
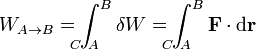
Se define asimismo la potencia desarrollada por la fuerza como el trabajo que realiza durante un tiempo dt, dividido por dicho intervalo
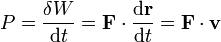
Aplicando la segunda ley de Newton la potencia desarrollada por una fuerza puede escribirse como la derivada respecto al tiempo de la energía cinética
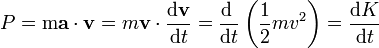
siendo K la energía cinética de la partícula
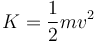
(donde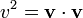 
es el módulo de la velocidad, o celeridad, al cuadrado).
Integrando respecto al tiempo obtenemos el teorema de las fuerzas vivas (o teorema trabajo-energía cinética):
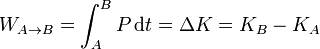
El trabajo realizado no tiene por qué ser necesariamente positivo. Si la partícula se ve frenada, su energía cinética disminuye y el trabajo resultante es negativo.
2 Fuerzas conservativas
3 Teorema de conservación de la energía mecánica
Cuando existe una energía potencial de la cual deriva la fuerza que actúa sobre una partícula se cumple la siguiente identidad
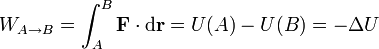
esto es, el trabajo realizado sobre la partícula es igual a la disminución de su energía potencial.
Combinando este teorema con el de las fuerzas vivas obtenemos
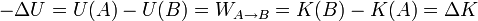
esto es, la que disminuye la energía potencial es igual a lo que aumenta la energía cinética (o viceversa). Reagrupando términos y definiendo la energía mecánica de la partícula como la suma de su energía cinética más la potencial obtenemos
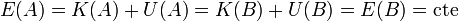
lo que se conoce como teorema de conservación de la energía mecánica:
- “En ausencia de fuerzas no conservativas, la energía mecánica de una partícula permanece constante.”
Este teorema deja de cumplirse cuando sobre la partícula actúan fuerzas no conservativas, como el rozamiento. Las fuerzas que reducen la energía mecánica (normalmente transformándola en calor) se conocen como fuerzas disipativas.
