Teoremas de conservación para una partícula

De Laplace

Revisión a fecha de 11:29 13 feb 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Constantes de movimiento
- 1.1 Constantes dependientes del tiempo
2 Cantidad de movimiento
3 Momento cinético
4 Trabajo y energía cinética
5 Energía mecánica

1 Constantes de movimiento

Una constante de movimiento o integral primera es una magnitud función de la posición, velocidad de la partícula (o de las partículas, si hay más de una), cuyo valores constante en el tiempo, pese a que la posición y la velocidad si son variables en el tiempo

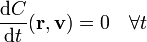
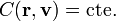
$\frac{\mathrm{d}C}{\mathrm{d}t}(\mathbf{r},\mathbf{v})=0\quad\forall t$ $\Rightarrow$ $C(\mathbf{r},\mathbf{v})=\mathrm{cte.}$

El ejemplo más intuitivo, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante.

Se denominan también integrales primeras, porque estas cantidades suelen obtenerse integrando una vez las ecuaciones de movimiento.

El hallazgo de una constante de movimiento en un problema simplifica la solución de éste, ya que permite establecer relaciones entre las variables y limita el número de soluciones posibles.

El valor concreto de una constante de movimiento puede calcularse a partir de las condiciones iniciales (o de los valores de la posicióin y velocidad en cualquier instante)

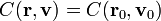
$C(\mathbf{r},\mathbf{v})=C(\mathbf{r}_0,\mathbf{v}_0)\,$

Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. Por ejemplo, en el movimiento planetario se conserva el llamado vector de Laplace-Runge-Lenz, que carece de interpretación sencilla.

1.1 Constantes dependientes del tiempo

Más en general, pueden encontrarse constantes de movimiento que además de la posición y velocidad, dependen del tiempo

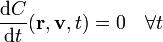
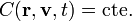
$\frac{\mathrm{d}C}{\mathrm{d}t}(\mathbf{r},\mathbf{v},t)=0\quad\forall t$ $\Rightarrow$ $C(\mathbf{r},\mathbf{v},t)=\mathrm{cte.}$

Su valor concreto lo da de nuevo la evaluación en un instante concreto

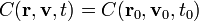
$C(\mathbf{r},\mathbf{v},t)=C(\mathbf{r}_0,\mathbf{v}_0,t_0)\,$

Puede parecer raro que se diga que una cantidad función del tiempo no depende del tiempo. Lo que se afirma es que aunque en la función puede aparecer la variable $t$ , el valor de la función es constante.

Por ejemplo, consideremos el caso de una partícula libre, para la cual F = 0

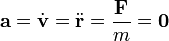
$\mathbf{a}=\dot{\mathbf{v}}=\ddot{\mathbf{r}}=\frac{\mathbf{F}}{m}=\mathbf{0}$

En este caso, la velocidad es una constante de movimiento

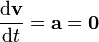
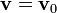
$\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}=\mathbf{a}=\mathbf{0}$ $\Rightarrow$ $\mathbf{v}=\mathbf{v}_0\,$

Si ahora construimos la cantidad vectorial, función del tiempo,

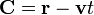
$\mathbf{C} = \mathbf{r}-\mathbf{v}t$

donde $\mathbf{r}$ y $\mathbf{v}$ son las velocidades instantáneas. ¿Cuánto vale su derivada respecto al tiempo?

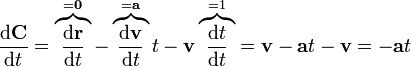
$\frac{\mathrm{d}\mathbf{C}}{\mathrm{d}t}=\overbrace{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}^{=\mathbf{0}}-\overbrace{\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}}^{=\mathbf{a}}t-\mathbf{v}\overbrace{\frac{\mathrm{d}t}{\mathrm{d}t}}^{=1} = \mathbf{v}-\mathbf{a}t-\mathbf{v}=-\mathbf{a}t$

Para una partícula libre la aceleración es nula, así que

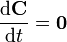
$\frac{\mathrm{d}\mathbf{C}}{\mathrm{d}t}=\mathbf{0}$

y por tanto 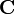$\mathbf{C}$ tiene siempre el mismo valor, aunque sea una función del tiempo. Hallamos este valor a partir de las condiciones iniciales.

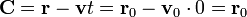
$\mathbf{C}=\mathbf{r}-\mathbf{v}t=\mathbf{r}_0-\mathbf{v}_0\cdot 0 = \mathbf{r}_0$

Y ahora, una vez que tenemos las dos constantes de movimiento, podemos depejar y escribir la solución

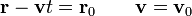
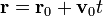
$\mathbf{r}-\mathbf{v}t= \mathbf{r}_0\qquad\mathbf{v}=\mathbf{v}_0$ $\Rightarrow$ $\mathbf{r}=\mathbf{r}_0+\mathbf{v}_0t$

Hemos llegado al resultado conocido de que una partícula libre describe un movimiento rectilíneo y uniforme siguiendo un camino más complicado que el habitual. Sin embargo, en muchos problemas más complicados, el uso de integrales primeras es el método más sencillo e intuitivo.

2 Cantidad de movimiento

Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad

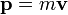
$\mathbf{p}=m\mathbf{v}\,$

La segunda ley de Newton tal como la formuló el propio Newton establece que la derivada respecto al tiempo de la cantidad de movimiento es la resultante de las fuerzas aplicadas sobre la partícula

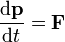
$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=\mathbf{F}$

Esta ecuación, para el caso de masa constante, se reduce a la más familiar versión 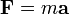$\mathbf{F}=m\mathbf{a}$ .

De esta expresión es inmediato que:

“La cantidad de movimiento de una partícula permanece constante cuando la fuerza es nula durante un intervalo de tiempo”

Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un sistema de partículas es extremadamente útil.

En ocasiones, no nos interesa tanto establecer la constancia de la cantidad de movimiento, sino saber cuánto varía. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante 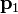$\mathbf{p}_1$ . Entonces es sometida a una fuerza 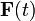$\mathbf{F}(t)$ durante un intervalo entre $t 1$ y $t 2$ (por ejemplo, durante una colisión, a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante 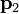$\mathbf{p}_2$ . Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. Integrando en la segunda ley de Newton obtenemos

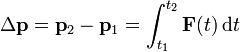
$\Delta \mathbf{p}=\mathbf{p}_2-\mathbf{p}_1 = \int_{t_1}^{t_2}\mathbf{F}(t)\,\mathrm{d}t$

Esta integral de la fuerza sobre un intervalo recibe el nombre de impulso, por tanto la igualdad anterior establece que “``el incremento de la cantidad de movimiento es igual al impulso recibido”. Esta relación, aparentemente trivial, tiene su importancia en la teoría de colisiones y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso.

3 Momento cinético

Se define el momento cinético (o momento angular)de una partícula respecto a un punto O como la cantidad

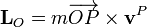
$\mathbf{L}_O=m\overrightarrow{OP}\times\mathbf{v}^P$

o, más sencillamente

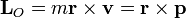
$\mathbf{L}_O = m \mathbf{r}\times\mathbf{v}=\mathbf{r}\times\mathbf{p}\,$

donde hay que entender que el vector de posición se mide respecto al punto O. Si queremos medir el momento angular respecto a un punto B el momento cinético cambia correspondientemente

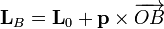
$\mathbf{L}_{B}=\mathbf{L}_0+\mathbf{p}\times\overrightarrow{OB}$

De la definición de momento cinético resulta proporcionalidad a la velocidad areolar

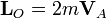
$\mathbf{L}_O=2m\mathbf{V}_A\,$

y por tanto la constancia del momento cinético equivale a la de la velocidad areolar.

Derivando el momento cinético respecto al tiempo

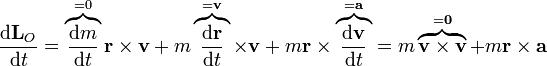
$\frac{\mathrm{d}\mathbf{L}_O}{\mathrm{d}t}=\overbrace{\frac{\mathrm{d}m}{\mathrm{d}t}}^{=0}\mathbf{r}\times\mathbf{v}+m\overbrace{\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}}^{=\mathbf{v}}\times\mathbf{v}+m\mathbf{r}\times\overbrace{\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}}^{=\mathbf{a}}=m\overbrace{\mathbf{v}\times\mathbf{v}}^{=\mathbf{0}}+m\mathbf{r}\times\mathbf{a}$

El producto 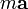$m\mathbf{a}$ es la resultante de las fuerzas que actúan sobre la partícula, por tanto

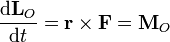
$\frac{\mathrm{d}\mathbf{L}_O}{\mathrm{d}t}=\mathbf{r}\times\mathbf{F}=\mathbf{M}_O$

Por tanto, la derivada respecto al tiempo del momento cinético respecto a un punto es igual al momento, respecto al mismo punto, de las fuerza neta que actúa sobre dicha partícula. Esto ocurrirá cuando la fuerza sea nula o cuando sea paralela al vector de posición (fuerza central). Por ello, podemos enunciar el teorema de conservación en la forma

“Si la fuerza neta que actúa sobre una partícula P es nula o es central con centro en un punto fijo O durante un cierto intervalo de tiempo, el momento cinético de la partícula respecto al punto O se mantiene constante durante dicho intervalo.”

3.1 Caso de una fuerza nula

Si 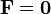$\mathbf{F} = \mathbf{0}$ el momento de la fuerza es naturalmente nulo y el momento angular es constante.

Podemos demostrar su constancia explícitamente. En ausencia de fuerza neta, una partícula sigue un movimiento rectilíneo y uniforme

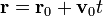
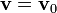
$\mathbf{r}=\mathbf{r}_0+\mathbf{v}_0t$ $\mathbf{v}=\mathbf{v}_0$

Hallando el momento angular en cada instante

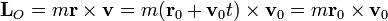
$\mathbf{L}_O=m\mathbf{r}\times\mathbf{v}=m(\mathbf{r}_0+\mathbf{v}_0t)\times\mathbf{v}_0=m\mathbf{r}_0\times\mathbf{v}_0$

ya que el producto vectorial de 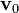$\mathbf{v}_0$ por sí mismo se anula. La última cantidad ya no depende del tiempo, sino que es el valor inicial del momento cinético y por tanto éste es constante. El módulo de este momento cinético es

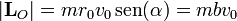
$|\mathbf{L}_O|= mr_0v_0\,\mathrm{sen}(\alpha) = mbv_0$

siendo $b$ el llamado parámetro de impacto: la mínima distancia del origen O a la que pasa la trayectoria rectilínea.

3.2 Caso de una fuerza central

Si la fuerza es todo momento paralela al vector de posición respecto al punto O, el producto vectorial 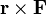$\mathbf{r}\times\mathbf{F}$ es nulo y el momento cinético respecto al punto O es constante

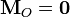
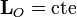
$\mathbf{M}_O = \mathbf{0}\,$ $\Rightarrow$ $\mathbf{L}_O=\mathrm{cte}\,$

Obsérvese que esta conservación sólo se aplica al momento cinético calculado respecto al centro de fuerzas. Para cualquier otro punto, el momento cinético no será constante.

Existen importantes ejemplos en física de fuerzas centrales y que por tanto satisfacen la conservación del momento cinético:

3.2.1 Ley de Hooke

Una fuerza $\mathbf{F}=-k\mathbf{r}$ es evidentemente paralela a $\mathbf{r}$ y el momento cinético respecto al punto de equilibrio se conserva. Podemos demostrarlo explícitamente. la ley horaria general de un oscilador armónico es

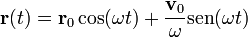
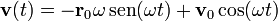
$\mathbf{r}(t) = \mathbf{r}_0\cos(\omega t)+\frac{\mathbf{v}_0}{\omega}\mathrm{sen}(\omega t)$ $\mathbf{v}(t) = -\mathbf{r}_0\omega\,\mathrm{sen}(\omega t)+\mathbf{v}_0\cos(\omega t)$

Hallando el momento cinético

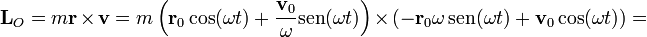
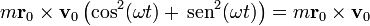
$\mathbf{L}_O=m\mathbf{r}\times\mathbf{v}=m\left(\mathbf{r}_0\cos(\omega t)+\frac{\mathbf{v}_0}{\omega}\mathrm{sen}(\omega t)\right)\times\left(-\mathbf{r}_0\omega\,\mathrm{sen}(\omega t)+\mathbf{v}_0\cos(\omega t)\right) =$ $m\mathbf{r}_0\times\mathbf{v}_0\left(\cos^2(\omega t)+\,\mathrm{sen}^2(\omega t)\right) = m\mathbf{r}_0\times\mathbf{v}_0$

resultando una constante igual al valor inicial del momento cinético.

En el caso general, el movimiento de un oscilador armónico es una elipse. La conservación del momento cinético (y por tanto de la velocidad areolar) establece que cuando la partícula se encuentra en el punto más alejado (el semieje mayor) la celeridad es mínima y cuando se encuentra más próxima 8en el semieje menor) su velocidad es máxima, cumpliéndose que $a v 1 = b v 2$ .

3.2.2 Ley de Gravitación universal

La atracción de un cuerpo por otro de gran masa, que puede considerarse fijo en el espacio, verifica aproximadamente la ley de la Gravitación Universal

$\mathbf{F}=-\frac{GMm}{r^2}\mathbf{u}_r$

Esta fuerza es también central y por tanto el momento cinético de un planeta en su órbita alrededor del Sol, respecto al Sol, es constante. Dada la proporcionalidad con la velocidad areolar, esto lleva a la Segunda Ley de Kepler:

“El radio vector de un planeta respecto al sol barre áreas iguales en tiempos iguales”

Por ello, la Tierra se mueve más rápido en invierno (en el hemisferio norte), en que el planeta pasa más cerca del Sol, que en verano, cuando se encuentra más alejado (por ello el intervalo entre el equinoccio de primavera, 21 de Marzo, y el de otoño, 23 de Septiembre, es 7 días más largo que el intervalo entre el equinoccio de otoño y el de primavera; el verano es más largo que el invierno)

El peso de un cuerpo en la superficie terrestre, en cambio, no verifica la conservación del momento cinético. Para un tiro parabólico desde el origen tenemos

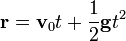
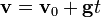
$\mathbf{r}=\mathbf{v}_0t+\frac{1}{2}\mathbf{g}t^2$ $\mathbf{v}=\mathbf{v}_0+\mathbf{g}t$

y el momento cinético es

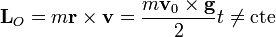
$\mathbf{L}_O= m\mathbf{r}\times\mathbf{v}=\frac{m\mathbf{v}_0\times\mathbf{g}}{2}t\neq\mathrm{cte}$

que no es constante, salvo en el caso en que la velocidad inicial y el peso sean paralelos (movimiento vertical).

Puede parecer raro que, si el peso es una manifestación de la fuerza gravitatoria no conserve el momento cinético. La razón es que, en el caso del peso, no estamos calculando el momento cinético respecto al centro de la fuerza (que sería el centro de la tierra), sino respecto a un punto de la superficie.

3.2.3 Movimiento circular

3.3 Conservación parcial del momento cinético

Existen ocasiones, como en el caso del peso mencionado anteriormente, en que el momento cinético no se conserva. Sin embargo, incluso en esos casos es a menudo obtener una ley de conservación más restringida.

Para ello, tenemos en cuenta que el momento cinético es un vector y posee tres componentes. Puede ocurrir que aunque el vector como tal no sea constante, una de sus componentes sí lo sea. Sea 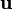$\mathbf{u}$ un vector unitario fijo. La componente del momento angular según la dirección de 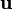$\mathbf{u}$ es

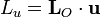
$L_{u}=\mathbf{L}_O\cdot\mathbf{u}\,$

Derivando aquí respecto al tiempo

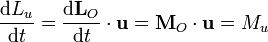
$\frac{\mathrm{d}L_u}{\mathrm{d}t}=\frac{\mathrm{d}\mathbf{L}_O}{\mathrm{d}t}\cdot\mathbf{u}=\mathbf{M}_O\cdot\mathbf{u}=M_u$

Si se anula la componente en la dirección de 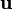$\mathbf{u}$ del momento de las fuerzas aplicadas, la componente del momento cinético en dicha dirección permanece constante.

Esto ocurre, en particular, si la fuerza mantiene una dirección constante. Por ejemplo, el peso puede escribirse como 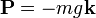$\mathbf{P}=-mg\mathbf{k}$ . En este caso

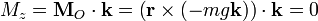
$M_z = \mathbf{M}_O\cdot\mathbf{k}=\left(\mathbf{r}\times(-mg\mathbf{k})\right)\cdot\mathbf{k}=0$

ya que el producto vectorial es perpendicular a la fuerza, esto es, al eje Z. Por tanto, una partícula sometida únicamente a la acción de su peso mantiene constante la componente $z$ de su momento cinético.

En la misma línea, pero un poco más complicado, es el caso del péndulo cónico. Este es un péndulo simple normal, pero que en lugar de limitarse a oscilar en un plano se le permite que se mueva también lateralmente, resultando en una trayectoria más o menos elíptica. La lenteja del péndulo está sometida a dos fuerzas: su peso y la tensión de la cuerda. La tensión de la cuerda va en la dirección del hilo, es central y por ello su momento es nulo. En particular, la componente $z$ de este momento será nula. El peso es siempre vertical y por ello, la componente $z$ del momento del peso es también nula, esto es

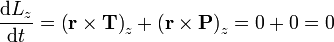
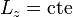
$\frac{\mathrm{d}L_z}{\mathrm{d}t}=\left(\mathbf{r}\times\mathbf{T}\right)_z +\left(\mathbf{r}\times\mathbf{P}\right)_z = 0 + 0=0$ $\Rightarrow$ $L_z=\mathrm{cte}\,$

y el péndulo cónico se mueve de forma que la componente $z$ de su momento cinético permanece constante.

4 Trabajo y energía cinética

5 Energía mecánica

Teoremas de conservación para una partícula

De Laplace

Contenido

1 Constantes de movimiento

1.1 Constantes dependientes del tiempo

2 Cantidad de movimiento

3 Momento cinético

3.1 Caso de una fuerza nula

3.2 Caso de una fuerza central

3.2.1 Ley de Hooke

3.2.2 Ley de Gravitación universal

3.2.3 Movimiento circular

3.3 Conservación parcial del momento cinético

4 Trabajo y energía cinética

5 Energía mecánica

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES