Potencial eléctrico debido a una polarización
De Laplace
Revisión a fecha de 21:28 6 feb 2010; Antonio (Discusión | contribuciones)
El potencial eléctrico debido a una polarización es la suma de los potenciales debidos a cada dipolo
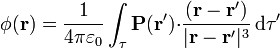
Esta integral suele ser difícil de calcular por métodos analíticos.
Una descripción alternativa es mediante las densidades de carga de polarización o de carga ligada, definidas como
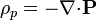
![\sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}]\,](/wiki/images/math/a/a/6/aa6172e549ca64c032e4c38ebbff7c6e.png)
La última fórmula, con el salto en la polarización, se aplica a una interfaz entre dos dieléctricos. Si uno de ellos es el vacío (en el
cual 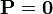 ), esta expresión se reduce a
), esta expresión se reduce a 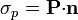 . En términos de ρp y σp el potencial es
. En términos de ρp y σp el potencial es
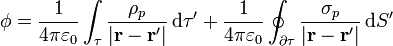
Empleando las cargas de polarización, las ecuaciones de la electrostática en presencia de dieléctricos se escriben como
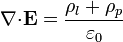

con las condiciones de salto
![\mathbf{n}{\cdot}[\mathbf{E}] = \frac{\sigma_l+\sigma_p}{\varepsilon_0}](/wiki/images/math/0/f/2/0f21e31dd3fd3bddd1df0ccafb74acab.png)
![\mathbf{n}\times
[\mathbf{E}]=\mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
siendo ρl y σl las densidades de carga libre, definidas como aquellas que no son de polarización.





