Esfera con hueco relleno de carga

De Laplace

1 Enunciado

Una esfera conductora de radio R tiene un hueco, también esférico, de radio R / 2, no siendo el hueco concéntrico con la esfera (sea a la distancia entre centros). Inicialmente la esfera se encuentra aislada y descargada.

1. Obtenga las expresiones del campo eléctrico y del potencial en todos los puntos del espacio cuando en el hueco se introduce una carga Q0 distribuida uniformemente en el volumen del hueco.
2. Manteniendo esta carga en el hueco, la superficie de la esfera conductora se conecta a una fuente de potencial de valor V₀. ¿Cuánto valen el campo y el potencial en todo el espacio una vez que se alcanza el equilibrio electrostático?
3. ¿Cuánta carga aporta el generador en el paso anterior?

2 Conductor descargado

Tenemos tres regiones: el hueco, el material conductor, y el exterior de la esfera conductora. El campo y el potencial en cada una son:

2.1 Exterior del conductor

Desde fuera del conductor solo vemos una esfera, de radio R en equilibrio electrostático. El problema del potencial, en esta región exterior es

con las condiciones de contorno

        

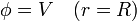
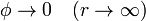
siendo V el potencial de la esfera, cuyo valor desconocemos por ahora y que calcularemos más tarde.

La solución de este problema es conocida:

        

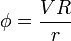
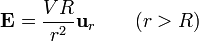
El valor de V lo obtenemos a partir de la carga. Si consideramos el flujo de a través una superficie esférica que envuelva a la esfera conductora, la ley de Gauss nos da la carga encerrada

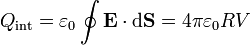
Por otro lado, la carga encerrada es solo la del hueco, pues el conductor está descargado. Por ello

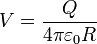
y el potencial y el campo en el exterior son

        

3 Conductor a tensión V₀

4 Carga suministrada