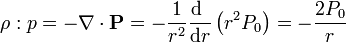Esfera polarizada radialmente

De Laplace

1 Enunciado

Se tiene una esfera de radio R, centrada en el origen, compuesta de un material con una polarización radial

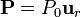
1. Calcule la distribución de cargas equivalente a esta polarización.
2. Determine los campos y en todo el espacio.

2 Cargas de polarización

2.1 De volumen

La densidad volumétrica de cargas equivalentes a la polarización del dieléctrico viene dada por la expresión

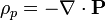
2.1.1 Exterior de la esfera

Fuera de la esfera la polarización es nula, por lo que no hay carga de polarización

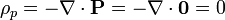
2.1.2 Interior de la esfera

Dado que el módulo de la polarización es uniforme, parecería que en el interior también la carga se anula, pero no es así. La polarización posee módulo uniforme, pero no dirección y sentido. La densidad de carga dentro es, empleando coordenadas esféricas,

2.2 Superficiales

2.3 Carga total

3 Campos

3.1 Desplazamiento eléctrico

3.2 Campo eléctrico

3.3 Aplicando la ley de Gauss