Campo magnético de una espira rectangular

De Laplace

1 Enunciado

Suponga una espira rectangular de lados a y b, por la cual circula una corriente continua I.

1. Halle el campo magnético en el centro de la espira. ¿A qué se reduce el resultado si a = b? ¿Y si ?

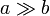Para el caso de una espira de lados 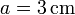, 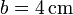por la que circula una corriente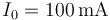

2. Halle el campo exacto en el centro de la espira.
3. Empleando la aproximación dipolar, calcule el campo a una distancia de 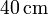del centro, en el eje de la espira.
4. A una distancia de 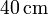del centro, a lo largo de una diagonal de la espira.

2 Solución

El campo debido a un segmento rectilíneo puede escribirse en la forma

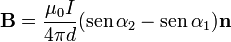
siendo α₁ y α₂ los ángulos con los que se ven los extremos del segmento desde el punto donde queremos hallar el campo, y es la normal al plano definido por el segmento y el punto de observación, con el sentido dado por la regla de la mano derecha.

En el caso de una espira rectangular, el campo en el centro irá en la dirección normal al plano de la espira, con el sentido dado por la regla de la mano derecha. La contribución de los cuatro lados va en el mismo sentido. Las contribuciones de lados opuestos se sumarán , dando el doble de cada una de ellas. Por tanto, sólo necesitamos calcular la contribución de un lado mayor (de longitud b) y de uno menor (de longitud a).

Para un lado de longitud b, la distancia del centro a dicho lado es a / 2, y los senos de los ángulos valen

        

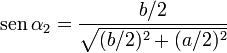
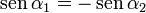
de forma que la contribución de este lado es

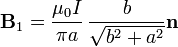
La contribución del lado corto será la correspondiente a intercambiar a por b

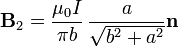
Y el campo total en el centro de la espira

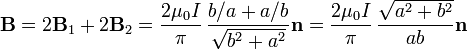
En el caso de una espira cuadrada, a = b este resultado se reduce a

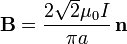
que corresponde a que los cuatro lados contribuyan por igual, siendo todos los senos iguales a .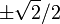

Si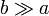

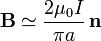
esto es, los lados pequeños y muy alejados tienen una contribución despreciable, mientras que los largos y próximos producen un campo equivalente al de dos hilos infinitamente largos.